Đề thi khảo sát chất lượng đầu năm môn Toán lớp 9

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 9 trường THCS Xuân Lai, Gia Bình năm 2015 - 2016 được TimDapAnsưu tầm và giới thiệu tới các bạn. Đề thi bao gồm đề kiểm tra đầu năm môn Toán, có đáp án đi kèm, là tài liệu tham khảo hữu ích dành cho các em học sinh từ lớp 8 lên lớp 9, giúp các em ôn tập và hệ thống lại kiến thức môn Toán hiệu quả.

Đề thi khảo sát chất lượng đầu vào môn Ngữ văn lớp 9 trường THCS Quảng Minh, Ba Đồn năm 2015 - 2016

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 9 trường THCS Cẩm Hoàng, Hải Dương năm 2015 - 2016

Đề thi khảo sát chất lượng đầu năm môn Ngữ văn lớp 9 trường THCS Quỳnh Lập, Nghệ An năm 2014 - 2015

Câu 1 (3 điểm):

1/ Tính giá trị của biểu thức x² – 1 tại x = 10

2/ Phân tích các đa thức sau thành nhân tử:

a) x² – 2x b) 2(x – y ) – y(x – y )

Câu 2 (2 điểm): Giải các phương trình sau:

a) x – 2 = 11 b) (x – 2)(x + 3) = 0

Câu 3 (1,5 điểm): Giải bài toán sau bằng cách lập phương trình:

Một người đi xe đạp từ A đến B với vận tốc trung bình 15 km/h. Lúc về người đó đi với vận tốc 12 km/h nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính quãng đường AB.

Câu 4 (3 điểm): Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD.

a) Chứng minh: ∆HAD ∼∆CDB.

b) Tính độ dài đoạn thẳng AH.

c) Gọi M, N, P lần lượt là trung điểm của BC, AH, DH. Tứ giác BMPN là hình gì? vì sao?

Câu 5 (0,5 điểm ): Cho x ≥ 0. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi khảo sát chất lượng đầu năm môn Toán lớp 9

Câu 1:

1/ Tính giá trị biểu thức:

Thay x = 10 vào biểu thức x² – 1 ta được: (0,25đ)

10² – 1 = 100 – 1 = 99 (0,5đ)

Vậy giá trị của biểu thức x² – 1 bằng 99 tại x = 10. (0,25đ)

2/ Phân tích đa thức thành nhân tử:

a) x² – 2x = x(x – 1) (1,0đ)

b) 2(x – y) – y(x – y) = (x – y)(2 – y) (1,0đ)

Câu 2:

a) x – 2 = 11 ⇔ x = 2 + 11 (0,5đ)

⇔ x = 13 (0,25đ)

Vậy phương trình có tập nghiệm: S = {13} (0,25đ)

b) (x – 2)(x + 3) = 0

Vây phương trình có tập nghiệm: S = {2; -3}

Câu 3:

Đổi 45 phút = 3/4 (giờ) (0,25đ)

Gọi độ dài quãng đường AB là x (x>0, km) (0,25đ)

Thời gian người xe đạp đi từ A đến B là: x/15 (giờ) (0,25đ)

Thời gian người xe đạp đi từ B về A là: x/12 (giờ) (0,25đ)

Vì thời gian về nhiều hơn thời gian đi là 3/4 (giờ), nên ta có phương trình: (0,25đ)

x/12 - x/15 = 3/4

⇔5x-4x=45

⇔x=45

<=>x = 45 thỏa mãn điều kiện của ẩn. Vậy quãng đường AB dài 45 km. (0,25đ)

Câu 4:

Hình vẽ đúng và ghi GT-KL (0,5đ)

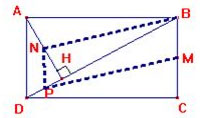
a) Xét ∆HAD và ∆CDB có: Góc AHD = Góc DCB = 90 và Góc ADH=DBC (So le trong).Vậy ∆HAD ∼∆CDB (g-g). (1,0đ)

b) Tính BD = 15cm (0,5đ)

Tính AH = 7,2cm (0,5đ)

c) Chứng minh được tứ giác BMPN là hình bình hành (0,5đ)

Câu 5:

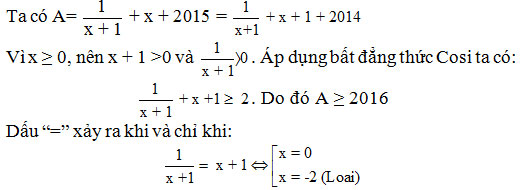
Vậy giá trị nhỏ nhất của A = 2016 khi x = 0