Đề thi khảo sát chất lượng đầu năm lớp 9 môn Toán

Đề thi khảo sát chất lượng đầu năm lớp 9 môn Toán năm 2013 - 2014 trường THCS Nghi Kiều, Nghệ An có đáp án là đề kiểm tra đầu năm môn Toán nhằm đánh giá chất lượng học sinh từ lớp 8 lên lớp 9. Hi vọng tài liệu này giúp các em học sinh ôn tập và củng cố kiển thức, chuẩn bị nền tảng vững chắc cho năm học cuối cấp THCS.

Đề thi khảo sát đầu năm Lớp 9 tỉnh Đăk Lăk môn Toán

Đề thi khảo sát chất lượng đầu năm lớp 9 huyện Bình Giang năm 2013 - 2014

Đề thi khảo sát chất lượng đầu năm lớp 9 môn Toán năm 2013-2014 trường THCS Phượng Kỳ, Hải Dương

Câu 1 (2,5 điểm): Giải các phương trình và bất phương trình sau:

a) 5x – 2 = 3x – 4; b) 2x + 4 = 0; c) 3x + 2 ≥ 4x + 14

Câu 2 (2,5 điểm) Cho biểu thức sau:

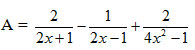
a) Tìm ĐKXĐ của biểu thức A;

b) Rút gọn biểu thức A

c) Tìm các giá trị của x để giá trị biểu thức A = 2

Câu 3 (1,5 điểm): Giải bài toán bằng cách lập phương trình:

Số sách ở giá thứ nhất gấp 4 lần số sách ở giá thứ hai. Nếu chuyển 18 quyển sách từ giá thứ nhất sang giá thứ hai thì số sách ở hai giá bằng nhau. Tìm số sách ban đầu ở mỗi giá.

Câu 4 (3,0 điểm): Cho tam giác ABC có AB = 2cm; AC = 4cm. Qua B vẽ đường thẳng cắt đoạn thẳng AC tại D sao cho góc ABD = góc ACB

a. Chứng minh tam giác ABD đồng dạng với tam giác ACB

b. Tính AD, DC

c. Gọi AH là đường cao của tam giác ABC, AE là đường cao của tam giác ABD. Chứng minh rằng: S_AHB = 4 S_SDE

Câu 5 (0,5 điểm): Cho a > b > 0 và 2a² +2b² = 5ab. Tính giá trị của biểu thức:

Đáp án đề thi khảo sát chất lượng đầu năm lớp 9 môn Toán

Câu 1 (2,5 điểm):

a) 5x – 2 = 3x – 4 ↔ 2x = -2 x = -1

Vậy nghiệm của pt là x = -1

b) 2x + 4 = 0 ↔ 2x = - 4 ↔ x = - 2

Vậy nghiệm của pt là x = - 2

c) 3x + 2 ≥ 4x + 14 ↔ 3x – 4x ≥ 14 - 2

↔ - x ≥ 12 ↔ x ≤ -12

Câu 2 (2,5 điểm)

a) TXĐ: x ≠ ±1/2

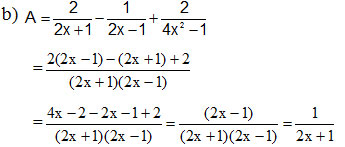
c) Với x ≠ ±1/2

Để A = 2 ↔ 1/(2x + 1) = 2 ↔ 2(2x + 1) = 1 ↔ 4x + 2 = 1 ↔ 4x = -1 ↔ x = -1/4 (TMĐK)

Câu 3 (1,5 điểm):

Gọi số sách ban đầu ở giá thứ hai là x (quyển); đk x > 0

Khi đó số sách ở giá thứ nhất là 4x (quyển);

Khi chuyển 18 quyển sách ở giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất và giá thứ hai lần lượt là 4x – 18 (quyển) và x + 18 (quyển).

Do sau khi chuyển thì số sách ở hai giá bằng nhau nên ta có pt:

4x – 18 = x + 18

Giải pt tìm được nghiệm x = 12 (TMĐK)

Trả lời số sách ở giá thứ hai là 12 quyển; số sách ở giá thứ nhất là 4.12 = 48 quyển.

Câu 4 (3,0 điểm)

HS vẽ hình, ghi GT và KL đúng

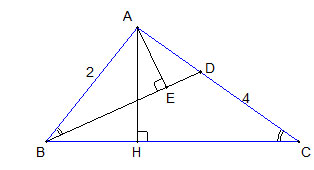
Xét ∆ABD và ∆ACB

Có: góc A chung

Góc ABD = góc ACB (gt)

→ ∆ABD đồng dạng ∆ACB (g.g)

b) ∆ABD đồng dạng ∆ACB (chứng minh câu a)

→ AD/AB = AB/AC

→ AD = AB²/AC = 2²/4 = 1 (cm)

DC = AC - AD = 4 - 1 = 3 (cm)

c. Ta có ∆ABD đồng dạng ∆ACB (chứng minh câu a)

Do đó tam giác vuông ABH đồng dạng tam giác vuông ADE (g-g)

→ S_ABH/S_ADE = (AB/AD)² = (2/1)² = 4. Vậy S_ABH = 4 S_ADE

Câu 5 (0,5 điểm)

Ta có 2a² + 2b² = 5ab

↔ 2a² + 4ab + 2b² = 9ab ↔ (a+b)² = 9ab/2

Tương tự : (a-b)² = ab/2

Do a > b > 0 → E > 0

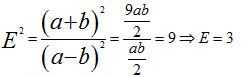
Ghi chú: Các cách giải khác đúng đều cho điểm tối đa của phần đó.