Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 trường THCS Long Xuyên, Hải Dương năm học 2014 - 2015 có đáp án đi kèm, giúp các bạn ôn tập lại kiến thức môn Toán lớp 7 và chuẩn bị tốt nhất cho chương trình học lớp 8. Mời các bạn tham khảo.

Đề thi khảo sát chất lượng đầu năm môn Ngữ văn lớp 8 trường THCS Long Xuyên, Hải Dương năm học 2014 - 2015

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 trường THCS Cao Viên, Hà Nội năm học 2016 - 2017

Bài 1. (2.5 điểm) Làm tính nhân:

a) 2x(x² – 3 x + 5)

b) (x – 2)(x + 2)

c) (x + 2y)²

Bài 2: ( 2.0 điểm) Tìm x, biết:

a) 6x(4x – 3) + 8x(5 – 3x) = 44

b) 9x² - 6x + 1 = 0

Bài 3: (2.0 điểm) Tính nhanh giá trị mỗi biểu thức sau:

a) 199² b) 47.53

c) 57² + 114.43 + 43² d. 5⁴3⁴ - (15² - 1)(15² + 1)

Bài 4. (3 điểm)

Cho tam giác ABC vuông cân tại A. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, vẽ BD vuông góc với BC sao cho BD = CB.

a) Tứ giác ABDC là hình gì? Vì sao?

b) Biết AB = 5cm. Tính CD.

Bài 5. (0,5 điểm) Rút gọn biểu thức: xⁿ – 2 (x² + 2y²) – y²(2x^{n – 2} + yⁿ – 2)

Đáp án đề thi khảo sát chất lượng đầu năm môn Toán lớp 8

Bài 1

a) 2x(x² – 3x + 5) = 2x³ – 6x² + 10x (0.5 điểm)

b) (x – 2)(x + 2) = x² – 2x + 2x – 4 = x² – 4 (0.5 điểm)

c) (x + 2y)² = x² + 2.x.2y + (2y)² = x² + 4xy + 4y² (1,0 điểm)

Bài 2

a) 6x(4x – 3) + 8x(5 – 3x) = 44

=> 24x² – 18x + 40x - 24x² = 44

=> 22x = 44

=> x = 2

b) Biến đổi được từ 9x² - 6x + 1 = 0

(3x - 1)² = 0 => x = 1/3

Bài 3

a) 199² = (200 - 1)² = 200² –2 .200.1+ 1² = 40000 – 400 = 39600 (0.5 điểm)

b) 47.53 = (50 - 3)(50 + 3) = 50² - 3² = 2500 - 9 = 2491 (0.5 điểm)

c) 57² + 114.43 + 43²

= 57² + 2.57.43 + 43²

= (57 + 43)² = 100² = 10000 (0.5 điểm)

d) 5⁴3⁴ - (15² - 1)(15² + 1) = 5⁴3⁴ - (15⁴ - 1²) = 15⁴ - 15⁴ + 1² = 1 (0.5 điểm)

Bài 4

Vẽ đúng hình (0,5 điểm)

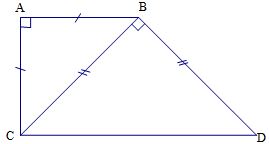
a) Ta có: ABC vuông cân tại A nên:

Ta có: DBC vuông cân tại B nên:

=> mà hai góc ở vị trí so le trong

=> AB // CD

=> Tứ giác ABDC là hình thang

Mà góc A = 90⁰

=> Hình thang ABDC là hình thang vuông.

b) Dựa vào định lý pytago tính được BC = 5√2 cm (0,5 điểm)

Dựa vào định lý pytago tính được CD = 10 cm (0,5 điểm)

Bài 5

x^{n – 2} (x² + 2y²) – y²(2x^{n – 2} + yⁿ – 2)
= xⁿ – 2 . x² + x^{n – 2} . 2y² – y² . 2x^{n – 2} – y² . y^{n – 2} (0,5 điểm)
= xⁿ – yⁿ (0,5 điểm)