Đề thi khảo sát chất lượng đầu năm lớp 8 môn Toán
Đề thi khảo sát chất lượng đầu năm lớp 8 môn Toán năm 2013 - 2014 trường THCS Vĩnh Tuy, Hà Giang là đề kiểm tra đầu năm môn Toán lớp 8 có đáp án. Đề thi được Tìm Đáp Án sưu tầm và đăng tải là tài liệu tham khảo hữu ích dành cho các em học sinh từ lớp 7 lên lớp 8, giúp các em ôn tập và hệ thống lại kiến thức môn Toán hiệu quả.
Đề thi khảo sát chất lượng đầu năm lớp 8 môn Toán năm 2013-2014 trường THCS Phượng Kỳ, Hải Dương
|
PHÒNG GD&ĐT BẮC QUANG TRƯỜNG THCS VĨNH TUY |
ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM 2013 - 2014 Môn: Toán 8 Thời gian: 90 phút (Không kể thời gian giao đề) |
I. TRẮC NGHIỆM (2 điểm): Khoanh tròn vào một chữ cái in hoa trước câu trả lời đúng.
Câu 1: Kết quả của phép nhân xy(x2+ x -1) là:
A. x3y + x2y + xy B. x3y - x2y - xy
C. x3y - x2y + xy D. x3y + x2y - xy
Câu 2: Biểu thức x3 + 3x2 + 3x + 1 là dạng khai triển của phép tính nào trong các phép tính dưới đây:
A. (x+1)3 B. (3x+1)3 C. (x+3)3 D. (x-1)3.
Câu 3: Tìm x, biết x2 - 25 = 0 ta được:
A. x = 25 B. x = 5 C. x = -5 D. x = 5 và x = -5
|
Câu 4: Giá trị của x trong hình vẽ sau là: A. 1000 B. 1200 C. 900 D. 1300 |
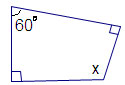 |
II. TỰ LUẬN (8 điểm)
Câu 1: (2 điểm) Làm tính nhân:
a/ x(x2 – 3x) b/ (x + 3)(x2 – 1)
Câu 2: (2 điểm) Tính:
a/ (2x + y)2 b) (2a - b)(2a + b)
Câu 3: (1 điểm) Viết biểu thức x + x2 + 1/4 dưới dạng bình phương của một tổng
Câu 4: (2 điểm) Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a) Tứ giác BDEC là hình gì? Vì sao?
b) Điểm D và điểm E nằm ở vị trí nào thì DE = 1/2 BC? Vì sao?
Đáp án đề thi khảo sát chất lượng đầu năm lớp 8 môn Toán
I/ TRẮC NGHIỆM (2 điểm): Mỗi ý đúng được 0,5 điểm
|
Câu |
1 |
2 |
3 |
4 |
|
Đáp án |
D |
A |
D |
B |
II/ TỰ LUẬN (8 điểm):
Câu 1
a/ x(x2 – 3x) = x3 – 3x2 (1đ)
b/ (x + 3)(x2 - 1) = x3 + 3x2 – x – 3 (1đ)
Câu 2
a/ (2x + y)2 = 4x2 + 4xy + y2 (1đ)
b/ (2a - b)(2a + b) = 4a2 - b2 (1đ)
Câu 3
x + x2 1/4 = (x + 1/2)2 (1đ)
Câu 4
Vẽ hình và ghi giả thiết + kết luận đúng: (0,5đ)
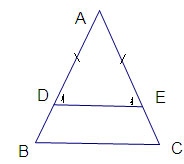
a/ Vì tam giác ABC cân tại A nên góc B = góc C (1) (0,25đ)
Vì AD = AE (gt) nên tam giác ADE cân tại A → góc D1 = góc E1 (2) (0,25đ)
Từ (1) và (2) suy ra góc B = góc D1 vì ở vị trí đồng vị nên DE // BC (3) (0,25đ)
Từ (1) và (3) suy ra BDEC là hình thang cân (0,25đ)
b/ Khi D và E lần lượt là trung điểm của AB và AC thì DE = 1/2 BC vì khi đó DE là đường trung bình của yam giác ABC. (1,5đ)











