Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi học sinh giỏi tỉnh Long An lớp 12 vòng 1 năm 2012 - 2013 môn Toán (Bảng B).

Đề thi học sinh giỏi môn Toán:

Câu 1: (6,0 điểm)

a) Giải hệ phương trình: 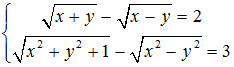với x, y thuộc i

b) Giải phương trình: với x thuộc i

Câu 2: (5,0 điểm)

a) Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC cân tại A, cạnh BC nằm trên đường thẳng có phương trình: 2x + y - 2 = 0. Đường cao kẻ từ B có phương trình: x + y + 1 = 0, điểm M(1; 1) thuộc đường cao kẻ từ đỉnh C. Xác định toạ độ các đỉnh của tam giác ABC.

b) Trong mặt phẳng cho bốn điểm phân biệt A,B,C,D sao cho bốn điểm đó không cùng nằm trên một đường thẳng. Chứng minh rằng:

Câu 3: (3,0 điểm)

Cho dãy số(u_n) xác định như sau:

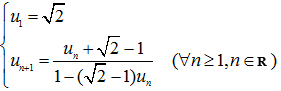
a) Chứng minh:

b) Tính: u₂₀₁₅

Câu 4: (3,0 điểm)

Cho ba số dương a, b c thỏa mãn abc = 1.Chứng minh rằng:

a. a² + b² + c² ≥ a + b + c

b.

Câu 5: (3,0 điểm)

Cho hệ phương trình: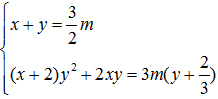

Tìm m để hệ phương trình có nhiều hơn hai nghiệm với x,y thuộc i