Vndoc.com xin giới thiệu đến các bạn: Đề thi học sinh giỏi Giải toán trên Máy tính Casio cấp tỉnh Đăk Nông môn Toán lớp 12 (2008 - 2009).

Đề thi học sinh giỏi môn Toán:

Quy định:

1/ Thí sinh được sử dụng hai loại máy tính CASIO fx-500MS và CASIO fx-570 MS, hoặc các loại máy có chức năng tương đương.

2/ Nếu không yêu cầu thêm hãy tính chính xác đến 4chữ số thập phân (ghi vào ô kết quả tất cả những chữ số đọc được trên màn hình)

3/ Thí sinh làm bài trực tiếp vào đề thi này. Nếu khung làm bài không đủ thì có thể làm tiếp ở mặt sau trang đề (lưu ý ghi rõ câu).

Bài 1 (2 điểm):

Cho hàm số . Tìm giá trị cực đại, giá trị cực tiểu.

Bài 2: (2 điểm)

Tìm min của hàm số

Bài 3: (2 điểm)

Tìm nghiệm gần đúng của phương trình sau: sin²2x + 5(sinx - cosx) = 2

Bài 4: (2 điểm)

Bố Hùng mất để lại cho Hùng 11000USD trong ngân hàng với lãi suất 0,73% một tháng. Mỗi tháng Hùng đến rút 60USD để sinh sống.

a) Hỏi sau một năm số tiền còn lại là bao nhiêu?

b) Nếu mỗi tháng rút 200USD thì sau bao lâu sẽ hết tiền?

Bài 5 (2 điểm):

Giải hệ phương trình: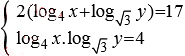

Bài 6: (2 điểm)

Cho nhị thức Newton .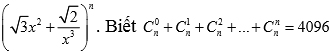

Hệ của số hạng chứa x⁴, x⁹ lần lượt là a, b. Tính tỉ số

Bài 7 (2 điểm):

Tìm giới hạn sau: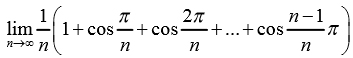

Bài 8: (2 điểm)

Cho ba đường thẳng lần lượt có phương trình là: d₁: 2x - 3y + 5 = 0; d₂: 3x - y - 7 = 0; d₃: 7x + 2y + 3 = 0.
. Tính tọa độ các điểm A, B, C và diện tích tam giác ABC. (Kết quả tính gần đúng lấy chính xác tới 7 chữ số thập phân)

Bài 9 (2 điểm):

a) Tìm số tự nhiên n biết tổng các chữ số của n bằng n² + 1999n + 8.

b) Tính gần đúng nghiệm thực đến hai chữ số thập phân của phương trình x¹³ – x⁶ + 3x⁴ – 3x² + 1 = 0

Bài10: (2 điểm)

Tính gần đúng thể tích và diện tích toàn phần của hình chóp đềuS.ABCD với cạnh đáy AB = 45cm, góc của mỗi cạnh bên và mặt đáy là α = 83⁰29'25'' (Kết quả tính gần đúng lấy chính xác tới 4 chữ số thập phân)