Đề thi học sinh giỏi môn Toán lớp 11 năm 2016

Đề thi học sinh giỏi môn Toán lớp 11 trường THPT Gia Viễn B, Ninh Bình năm học 2015 - 2016 là đề thi học sinh giỏi cấp trường môn Toán lớp 11. Tài liệu bao gồm đề thi và đáp án, thuận tiện cho các bạn luyện tập và kiểm tra lại kết quả sau khi làm bài, hi vọng giúp các bạn ôn thi học sinh giỏi lớp 11 hiệu quả.

Đề thi học sinh giỏi môn Toán lớp 11 trường THPT Tam Quan năm 2015 - 2016

Đề thi học sinh giỏi tỉnh Bạc Liêu môn Toán lớp 11 (Năm học 2010 - 2011) - Có đáp án

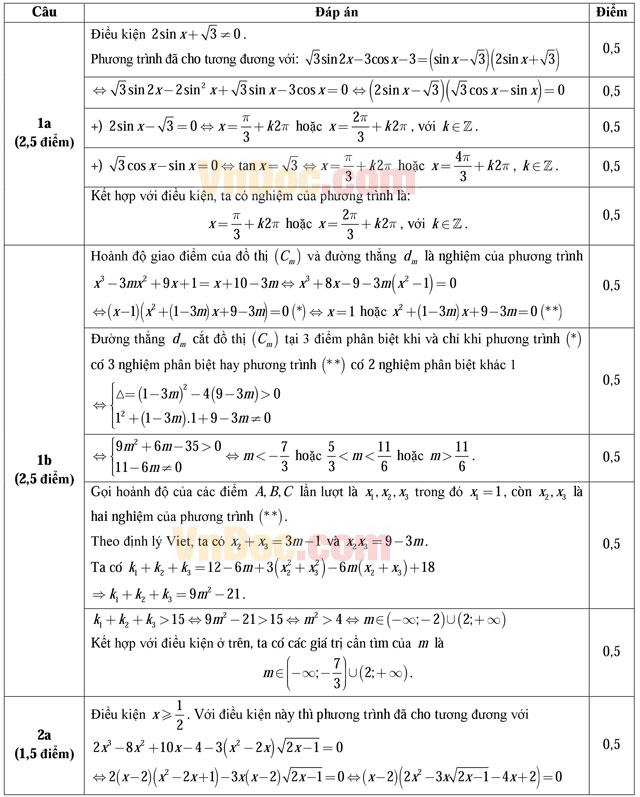
Câu 1 (5,0 điểm)

a) Giải phương trình:

b) Cho hàm số y = x³ - 3x² + 9x + 1, có đồ thị (C_m), với m là tham số. Tìm giá trị của tham số m để đường thẳng d_m: y = x + 10 - 3m cắt đồ thị (C_m) tại 3 điểm phân biệt A, B, C. Gọi k₁, k₂, k₃ là hệ số góc tiếp tuyến của (C_m) lần lượt tại A, B, C. Tìm giá trị của m để k₁ + k₂ + k₃ >15.

Câu 2 (3,0 điểm)

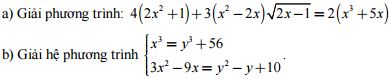
Câu 3 (3,0 điểm).

a) Tìm hệ số của số hạng chứa x²⁶ trong khai triển nhị thức Niu-tơn của , biết rằng n là số nguyên dương thỏa mãn .

b) Chứng minh rằng phương trình x³ - 3x + 1 = 0 có 3 nghiệm phân biệt x₁, x₂, x₃ (x₁ < x₂ < x₃) thỏa mãn hệ thức .

Câu 4 (2,0 điểm). Giải bất phương trình .

Câu 5 (2,5 điểm). Cho hình chóp S.ABCD. có đáy là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M N, lần lượt là trung điểm của các cạnh SB và CD. Chứng minh rằng AM vuông góc với BN. Tính khoảng cách từ điểm A đến mặt phẳng (SMN).

Câu 6 (2,5 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có AC = 2BD và đường tròn nội tiếp hình thoi có phương trình là . Biết rằng đường thẳng AB đi qua điểm M (1; 5). Tìm tọa độ đỉnh A, biết điểm A có hoành độ âm.

Câu 7 (2,0 điểm). Cho các số thực dương a, b, c thỏa mãn điều kiện ab + bc + ca = 3. Tìm giá trị nhỏ nhất của biểu thức:

Đáp án đề thi học sinh giỏi môn Toán lớp 11 năm 2016