Đề thi học sinh giỏi cấp huyện môn Toán lớp 9
Đề thi học sinh giỏi cấp huyện môn Toán lớp 9 phòng GD&ĐT Thạch Hà, Hà Tĩnh năm 2016 - 2017 là đề tham khảo dành cho các bạn học sinh và thầy cô nghiên cứu, học tập tốt môn Toán lớp 9 cũng như luyện tập và làm quen với nhiều đề học sinh giỏi hơn nhằm chuẩn bị tốt nhất cho các kì thi sắp diễn ra. Mời các bạn tham khảo.
Đề thi học sinh giỏi môn Ngữ văn lớp 9 phòng GD&ĐT Thái Hòa, Nghệ An năm 2016 - 2017
| PHÒNG GD&ĐT THẠCH HÀ |
ĐỀ THI HỌC SINH GIỎI HUYỆN NĂM HỌC 2016 – 2017 Môn thi: Toán 9 Thời gian làm bài 150 phút |
Câu 1:
a) Tính giá trị của đa thức 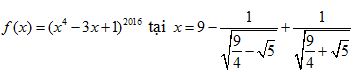
b) So sánh 
c) Tính giá trị biểu thức: ![]()
d) Biết là số vô tỉ, hãy tìm các số nguyên a, b thỏa mãn: ![]()
Câu 2: Giải các phương trình sau: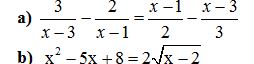
Câu 3:
a) Cho đa thức P(x) = ax3 + bx2 + cx + d với a, b, c, d là các hệ số nguyên. Chứng minh rằng nếu P(x) chia hết cho 5 với mọi giá trị nguyên của x thì các hệ số a, b, c, d đều chia hết cho 5
b) Tìm nghiệm nguyên của phương trình: x2 – xy + y2 – 4 = 0
c) Cho n là số tự nhiên lớn hơn 1. Chứng minh rằng n4 + 4n là hợp số.
Câu 4:
a) Chứng minh rằng ![]()
b) Cho a, b, c là 3 số dương thỏa mãn điều kiện 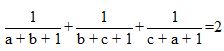
Tìm giá trị lớn nhất của tích (a + b)(b + c)(c + a).
Câu 5: Cho ΔABC nhọn, có ba đường cao AD, BI, CK cắt nhau tại H. Gọi chân các đường vuông góc hạ từ D xuống AB, AC lần lượt là E và F
a) Chứng minh rằng: AE.AB = AF.AC
b) Giả sử HD = 1/3AD. Chứng minh rằng: tanB.tanC = 3
c) Gọi M, N lần lượt là chân đường vuông góc kẻ từ D đến BI và CK. Chứng minh rằng: 4 điểm E, M, N, F thẳng hàng.
Đáp án đề thi học sinh giỏi cấp huyện môn Toán lớp 9















