Bài 1: ( 4 điểm)

1/ Không sử dụng máy tính, hãy thực hiện phép tính: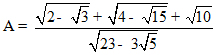

2/ Cho biểu thức:

a/ Tìm điều kiện xác định và rút gọn B.

b/ Tìm giá trị lớn nhất của B và giá trị x tương ứng.

Bài 2: (5 điểm)

1/ Tìm hệ số a > 0 sao cho các đường thẳng y = ax – 1 ; y = 1 ; y = 5 và trục tung tạo thành hình thang có diện tích bằng 8 (đơn vị diện tích).

2/ Cho các số x, y, z khác 0 thỏa mãn đồng thời

Tính giá trị của biểu thức P = (x + 2y + z)²⁰¹².

Bài 3: (5 điểm)

Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF (DBC, EAC, F AB) cắt nhau tại H và cắt đường tròn (O) theo thứ tự ở M, N, K. Chứng minh rằng:

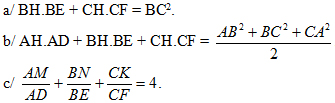
Bài 4: (3 điểm)

Cho đoạn thẳng CD = 6 cm, I là một điểm nằm giữa C và D ( IC > ID). Trên tia Ix vuông góc với CD lấy hai điểm M và N sao cho IC = IM, ID = IN, CN cắt MD tại K (K thuộc MD), DN cắt MC tại L (L thuộc MC). Tìm vị trí của điểm I trên CD sao cho CN.NK có giá trị lớn nhất.

Bài 5: (3 điểm)

Tìm các cặp số (x; y) nguyên dương thỏa mãn: xy + 2x = 27 – 3y.