Bài 1. (2,0 điểm)

Cho biểu thức: 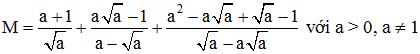với a > 0, a # 1.

a) Chứng minh rằng M>4

b) Với những giá trị nào của a thì biểu thức 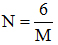nhận giá trị nguyên?

Bài 2. (2,0 điểm)
a) Cho các hàm số bậc nhất: y = 0,5x + 3. y = 6 - x, và y = mx có đồ thị lần lượt là các đường thẳng (d1), (d2) và (dm). Với những giá trị nào của tham số m thì đường thẳng (dm) cắt hai đường thẳng (d1) và (d2) lần lượt tại hai điểm A và B sao cho điểm A có hoành độ âm còn điểm B có hoành độ dương?
b) Trên mặt phẳng tọa độ Oxy, cho M và N là hai điểm phân biệt, di động lần lượt trên trục hoành và trên trục tung sao cho đường thẳng MN luôn đi qua điểm cố định . Tìm hệ thức liên hệ giữa hoành độ của M và tung độ của N; từ đó, suy ra giá trị nhỏ nhất của biểu thức

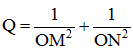
Bài 3. (2,0 điểm)

a) Giải hệ phương trình: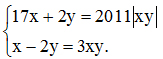

b) Tìm tất cả các giá trị của x, y, z sao cho: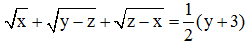

Bài 4. (3,0 điểm)
Cho đường tròn (C ) với tâm O và đường kính AB cố định. Gọi M là điểm di động trên (C ) sao cho M không trùng với các điểm A và B. Lấy C là điểm đối xứng của O qua A. Đường thẳng vuông góc với AB tại C cắt đường thẳng AM tại N. Đường thẳng BN cắt đường tròn (C ) tại điểm thứ hai là E. Các đường thẳng BM và CN cắt nhau tại F.
a) Chứng minh rằng các điểm A, E, F thẳng hàng.
b) Chứng minh rằng tích AM.AN không đổi.
c) Chứng minh rằng A là trọng tâm của tam giác BNF khi và chỉ khi NF ngắn nhất.

Bài 5. (1,0 điểm)
Tìm ba chữ số tận cùng của tích của mười hai số nguyên dương đầu tiên.