Bài 1: (4 điểm)

1/ Không sử dụng máy tính, thực hiện phép tính:

2/ Cho biểu thức:

Tìm giá trị lớn nhất của biểu thức B và giá trị x tương ứng

Bài 2: (5 điểm)

1/ Cho hàm số y = ax² (a # 0) có đồ thị là (P) đi qua M(-1;2). Trên (P) lấy A và B có hoành độ tương ứng là 1 và 2. Xác định m để đường thẳng y = mx +5 song song với đường thẳng AB

2/ Tìm x thỏa mãn: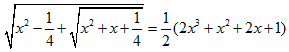

Bài 3: (5 điểm)

Cho tam giác ABC có ba góc đều nhọn có AB < AC nội tiếp đường tròn O bán kính R. Ba đường cao AD,BE,CF cắt nhau tại H

a/ Chứng minh H là tâm đường tròn nội tiếp tam giác DEF

b/ Kẻ đường kính AK của đường tròn O. Gọi S là diện tích tam giác ABC

Chứng minh:

c/ Gọi M là trung điểm BC. Chứng minh: tứ giác DFEM là nội tiếp

Bài 4: (3 điểm)

Cho điểm M nằm trong tam giác ABC có BC = a, AC = b, AB = c. Gọi các khoảng cách từ M đến ba cạnh BC, AC, AB tương ứng là x,y,z .

Hãy xác định vị trí M trong tam giác sao cho biểu thức: đạt giá trị nhỏ nhất

Bài 5: (3 điểm)

Tìm một số chính phương có bốn chữ số, mỗi chữ số nhỏ hơn 9. Biết rằng khi tăng mỗi chữ số thêm một đơn vị thì số mới được tạo thành cũng là số chính phương.