Đề thi học kì 1 môn Toán lớp 12

Đề thi học kì 1 môn Toán lớp 12 tỉnh Quảng Nam năm học 2015 - 2016 là đề kiểm tra học kì I môn Toán lớp 12 dành cho các bạn và thầy cô tham khảo, ra đề cũng như ôn tập, hệ thống kiến thức Toán 12, ôn thi chuẩn bị cho kì thi THPT Quốc gia sắp tới. Mời các bạn tham khảo đề thi ôn luyện và học tập.

Bộ đề thi học kì 1 môn Toán lớp 12 năm học 2016 - 2017 (Số 1)

Đề thi học kì 1 môn Toán lớp 12 trường THPT Yên Lạc 2, Vĩnh Phúc năm học 2015 - 2016

Đề thi học kì 1 môn Toán lớp 12 năm học 2015 - 2016 Thành phố Cần Thơ

Câu 1 (2,0 điểm).

Cho hàm số

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(3; 4).

Câu 2 (2,0 điểm).

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) = x⁴ - 8x² + 3 trên đoạn [–1; 3].

b) Xác định giá trị của tham số m để hàm số sau đạt cực đại tại x = 1:

y = 1/3x³ - mx² + (m² - 4)x + 2

Câu 3 (1,0 điểm).

Tìm tập xác định và tính đạo hàm của hàm số

Câu 4 (2,0 điểm).

a) Giải bất phương trình: 3^x – 4.3^{1 – x} + 1 ≥ 0.

b) Giải phương trình: log₂x + 1/2 log_√2(x - 1) = 1 - log_1/2(x + 2).

Câu 5 (1,0 điểm).

Cho hình trụ có bán kính đáy r = 10 cm và chiều cao h = 30 cm. Tính diện tích xung quanh của hình trụ và thể tích khối trụ tạo nên bởi hình trụ đó.

Câu 6 (2,0 điểm).

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60⁰.

a) Tính theo a thể tích khối chóp S.ABC.

b) Gọi G là trọng tâm tam giác SAC. Tính theo a diện tích mặt cầu có tâm G và tiếp xúc với mặt phẳng (SAB).

Đáp án đề thi học kì 1 môn Toán lớp 12

Câu 1.

a) (1.5 điểm)

• Tập xác định: D = R\{2}
• 
• Vì y' < 0, ∀x ≠ 2 nên hàm số nghịch biến trên mỗi khoảng (–∞;2), (2;+∞).
• Giới hạn và tiệm cận đúng
• Bảng biến thiên
• Đồ thị

b) (0.5 điểm)

• Hệ số góc TT của (C) tại M là y'(3) = –3.
• Phương trình tiếp tuyến của (C) lại M là: y – 4 = –3(x – 3) hay y = –3x + 13.

Câu 2.

a) (1.0 điểm)

• f '(x) = 4x³ - 16
• 
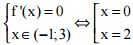
• f(0) = 3; f(2) = –13; f(–1) = –4; f(3) = 12
• Kết luận đúng.

b) (1.0 điểm)

• y' = x² – 2mx + m² – 4
• Giả sử hàm số đạt cực đại tại x = 1 thì: y'(1)=0 ⇔ m² – 2m – 3 = 0 ⇔ m = –1 hoặc m = 3
• Ngươc lại, chứng minh được m = –1 hàm số đạt cực tiểu tại x = 1, m = 3 hàm số đạt cực đại tại x = 1 và kết luận đúng.

(CM đúng một trường hợp:0.25; CM trường hợp còn lại và kết luận đúng: 0.25)

Câu 3

• Hàm số đã cho xác định khi: 1 – lnx > 0 ⇔ lnx < 1 ⇔ 0 < x < e. Tập xđ: D = (0; e)
• 

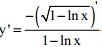
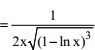
Câu 4.

a) (1.0 điểm) 3^x – 4.3^{1 – x} + 1 ≥ 0 (1)

• (1) ⇔ 3^2x + 3^x – 12 ≥ 0 (1a)
• Đặt t = 3^x, t > 0, (1a) trở thành: t² + t – 12 ≥ 0 ⇔ t ≤ –4 (loại) hoặc t ≥ 3 (thỏa t > 0).
• Với t ≥ 3 thì 3^x ≥ 3 ⇔ x ≥ 1

b) (1.0 điểm) Ký hiệu phương trình đã cho là (2).

• ĐK: x > 1
• 2 ⇔ log₂x + 1/2 log_√2(x - 1) = 1 - log_1/2(x + 2)
• ⇔ ... ⇔ x² – x = 2x + 4 ⇔ x² – 3x – 4 = 0⇔ x = –1 hoặc x = 4
• Kết hợp với điều kiện x > 1 suy ra phương trình (2) có một nghiệm x = 4.

Câu 5

• Diện tích xung quanh của hình trụ: S_xq = 2πrh = 600π (cm²).
• Thể tích khối trụ: V = πr²h = 3000π (cm³).

Câu 6.

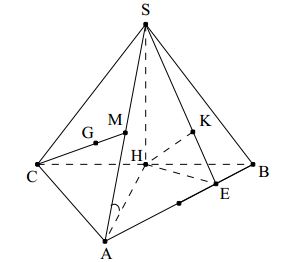
a) (1.0 điểm)

+ Xác định được góc (SA,(ABC)) = góc SAH = 60⁰.

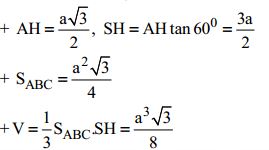
b) (1.0 điểm)

• Lập luận được bán kính mặt cầu là: R = d(G,(SAB)) = 1/3 d(C,(SAB)) = 2/3 d(H,(SAB))
• Gọi E là hình chiếu của H trên AB và K là hình chiếu của H trên SE. Chứng minh được: HK ⊥ (SAB)
• 
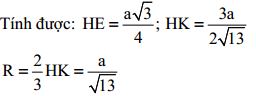
• Diện tích mặt cầu: