Đề thi thử học kỳ 1 môn Toán lớp 12

Tìm Đáp Án xin giới thiệu tới bạn đọc tài liệu: Đề thi thử học kỳ 1 môn Toán lớp 12 năm học ‎‎2017 - 2018, với bộ câu hỏi trắc nghiệm gồm 50 câu để phục vụ các bạn học sinh rèn luyện giải bài tập Toán 12 một cách hiệu quả hơn. Mời thầy cô cùng các bạn học sinh tham khảo.

Học tốt Toán lớp 12: Đề thi thử học kỳ 1 môn Toán lớp 12

Câu 1. Đạo hàm của hàm số là?

Câu 2. Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. Diện tích xung quanh của hình nón là?

Câu 3. Tìm các khoảng đồng biến của hàm số y = 1/3x³ - 4x + 5

A. (-oo; -2) và (2; +oo)

B. (-2; 2)

C. (-oo; 2)

D. (-2; +oo)

Câu 4. Tập nghiệm của bất phương trình: log₂x + log₃x < 1+ log₂x.log₃x là?

A. (2;3)

B. (0; 2) ∪ (3; +oo)

C. (-oo; 2) ∪ (3; +oo)

D. (-oo; 0) ∪ (2;3)

Câu 5. Giá trị cực tiểu của hàm số y = x³ - 3x² +1 là:

A. 2

B. -1

C. -3

D. 1

Câu 6. Cho hình chóp S.ABC có ba cạnh đôi một vuông góc tại A và SA = a, AB = b, AC = c. Tích V của khối chóp là:

A. V = abc

B. V = 1/6 abc

C. V = abc/3

D. V = 3abc

Câu 7. Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng y = m + 3 cắt đồ thị hàm số y = 2Ιx³Ι - 9x² + 6 tại 4 điểm phân biệt.

A. -24 < m ≤ 6

B. m > -21

C. -21 < m < 6

D. -24 < m < 3

Câu 8. Khẳng định nào dưới đây là khẳng định SAI?

A. Quay một tam giác nhọn xung quanh cạnh của nó không thể tạo ra hình nón.

B. Quay tam giác đều quanh đường cao của nó luôn tạo ra một hình nón.

C. Quay hình vuông xung quanh cạnh của nó luôn sinh ra hình trụ .

D. Quay đường tròn xung quanh một dây cung của nó luôn tạo ra một hình cầu

Câu 9. Cường độ một trận động đất được cho bởi công thức M = log A - log A₀, với A là biên độ rung chấn tối đa và A₀ là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ đo được 8 độ Richter. Trong cùng năm đó, trận động đất khác ở Nhật Bản có cường độ đo được 6 độ Richer. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ trận động đất ở Nhật bản?

A. 100 lần

B. 1000 lần

C. 2 lần

D. 10 lần

Câu 10. Tìm nguyên hàm F(x) của hàm số f(x) = sin³ x biết F(0) = 1

Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD là:

Câu 13. Tìm tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = -x² + 4x - 2m + 3 bằng 1.

A. m = 3

B. m = 1

C. m = 2

D. m =

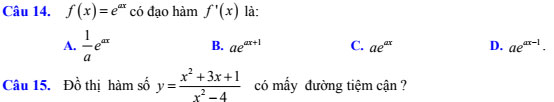
A. 3

B. 0.

C. 2

D. 1

Câu 16. Hình sau là đồ thị của hàm số y = -x⁴ + 4x². Dựa vào đồ thị hãy tìm tất cả các giá trị thực của tham số m sao cho phương trình x⁴ - 4x² + m = 0 có bốn nghiệm phân biệt.

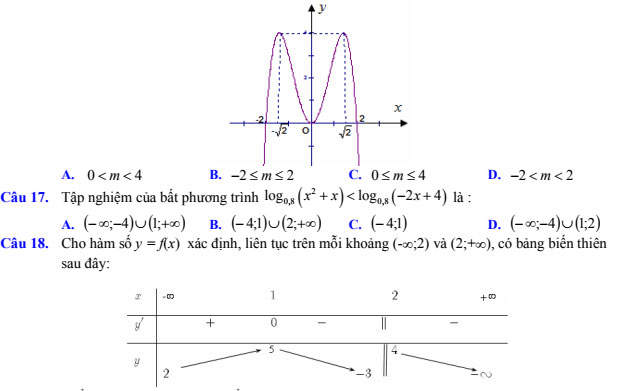
Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng (-oo;1)

B. Hàm số nghịch biến trên khoảng (5; -3)

C. Giá trị cực đại của hàm số bằng 5

D. Giá trị lớn nhất của hàm số trên khoảng (0;2) bằng 5

Câu 19. Một công ty muốn thiết kế bao bì để đựng sữa với thể tích 1dm³ . Bao bì được thiết kế bởi một trong hai mô hình sau: dạng hình hộp chữ nhật có đáy là hình vuông hoặc dạng hình trụ và được sản xuất cùng một nguyên vật liệu. Hỏi thiết kế theo mô hình nào sẽ tiết kiệm được nguyên vật liệu nhất? Và thiết kế mô hình đó theo kích thước như thế nào?

A. Hình hộp chữ nhật có cạnh bên bằng 1/4 dm và cạnh đáy 2dm.

B. Hình lập phương có cạnh bằng 1dm.

C. Hình trụ có bán kính đáy dm và chiều cao bằng bán kính đáy.

D. Hình trụ có bán kính đáy dm và chiều cao bằng đường kính đáy.

Câu 20. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x⁴ + 2(2m - 3)x² - 8(m -1)x + 2 có 3 điểm cực trị.

Câu 21. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, AB = a. Cạnh bên SA vuông góc với mặt đáy. Góc giữa SB và mặt đáy bằng 45⁰ . Thể tích của khối cầu ngoại tiếp hình chóp S.ABC là:

Câu 22. Biết một trong các hàm số được cho trong các phương án A, B, C, D dưới đây có đồ thị như hình vẽ. Đó là hàm số nào?

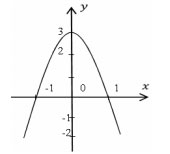
A. y = -x⁴ + 2x² + 3

B. y = -x⁴ - x² + 3

C. y = -x⁴ - 2x² + 3

D.y = x⁴ - 4x³ + 3

Câu 23. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 2x - 3m + 2 có cực trị.

A. m > 0

B. m ≤ 0

C. m < 0

D. m ≥ 0

Câu 24. Cho hàm số f (x) có tính chất f / (x) ≤ 0, ∀x ∈(0;5) và f / (x) = 0, ∀x ∈ (1;3). Hỏi khẳng định nào sau đây là khẳng định sai?

A. Hàm số f (x) nghịch biến trên khoảng (3;5)

B. Hàm số f (x) nghịch biến trên khoảng (0;5)

C. Hàm số f (x) nghịch biến trên khoảng (0;1)

D. Hàm số f (x) là hàm hằng trên khoảng (1;3)

Câu 25. Khẳng định nào sau đây SAI?

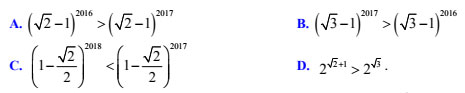
Câu 26. Một hình trụ có trục OO' = 2 , ABCD là hình vuông có cạnh bằng 8 có đỉnh nằm trên hai đường tròn đáy sao cho tâm của hình vuông trùng với trung điểm của OO'. Thể tích của hình trụ bằng bao nhiêu?

Câu 27. Hình chóp S.ABC có SB = SC = BC = CA = a. Hai mặt phẳng ( ABC ) và ( ASC ) cùng vuông góc với mặt phẳng (SBC ). Thể tích hình chóp là:

Câu 31. Tổng các nghiệm của phương trình: 4^x+1 - 6.2^x+1 + 8 = 0 là:

A. 3

B. 5

C. 6

D. 1

Câu 32. Hàm số y = ΙxΙ³ - 3x + 5 có bao nhiêu điểm cực trị?

A. 2

B. 3

C. 1

D. 0

Câu 33. Tập nghiệm của bất phương trình là:

A. (- oo;-2) ∪ (- 2;+oo)

B. (- oo;-2)

C. (- 2;+ô)

D. Ø

Câu 34. Cho hình nón có bán kính đáy bằng 3 cm, chiều cao bằng 9 cm. Thể tích của khối nón là:

A. 72 (cm³)

B. 216 (cm³)

C. 27 (cm³)

D. 81 (cm³)

Câu 35. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x - 5/x - 3 trên đoạn [4; 7] là:

A. M = 1, m = 1/2

A. M = 1/2, m = -1

C. M = 1, m = - 1/2

D. M = 1/2, m = - 1

Câu 36. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x² - 2lnx trên [e^-1;e] lần lượt là:

A. (1/e)² + 2 và 1

B. 1 và 0

C. Đáp số khác.

D. e² - 2 và 1

Câu 37. Phương trình tiếp tuyến của đồ thị hàm số y = 2^x tại điểm A(2; 4) là:

A. y = 4x ln 2 - 8ln 2 + 4

C. y = x ln 2 - 8 ln 2 + 4

B. y = 4x ln 2 + 8 ln 2 + 4

D. y = x ln 2 + 8 ln 2 + 4

Câu 38. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a = 3cm. Cạnh SA vuông góc với mặt phẳng (ABC) và SA = 6cm. Thể tích khối cầu ngoại tiếp hình chóp bằng:

Câu 39. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = mx - sin x đồng biến trên R.

A. m < 1

B. m > 1

C. m ≤ 1

D. m ≥ 1

Câu 40. Cho hình hộp chữ nhật ABCD.A' B'C' D' có diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt bằng 20cm², 28cm2, 35cm². Bán kính mặt cầu ngoại tiếp hình hộp bằng:

Câu 41. Khối đa diện đều mà mỗi mặt là đa giác đều n cạnh và mỗi đỉnh là đỉnh chung của p cạnh được gọi là khối đa diện đều loại {n; p} . Khối bát diện đều là khối đa diện đều loại:

A. {3; 5}

B. {4; 3}

C. {5; 3}

D. {3; 4}

Câu 42. Tiếp tuyến của đồ thị hàm số y = ln(x² +1) tại điểm A(1; ln 2) có hệ số góc là:

A. k = -1

B. k = ln 2

C. k = 1

D. k =1/ln 2

Câu 43. Giá trị nhỏ nhất của hàm sốy = 2 ΙxΙ trên đoạn [-1;1] là:

A. 1 2

B. 1

C. 2

D. 4

Câu 44. Giá trị nhỏ nhất của hàm số y = 4x + 5 + 4/x trên nửa khoảng (1/2;3) là?

A. 13

B. -5

C. 15

D. -3

Câu 45. Phương trình log₂ (x - 3) + log₂ (x -1) = 3 có nghiệm là:

A. x = 5

B. x = 7

C. x = 11

D. x = 9

Câu 46. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau đây:

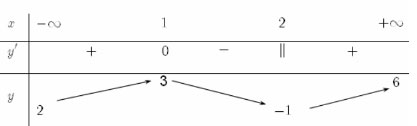
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đạt cực tiểu tại x = 1

B. Hàm số nghịch biến trên khoảng (1; 2).

C. Hàm số đã cho có đúng một cực trị.

D. Hàm số đã cho có giá lớn nhất bằng 6 và giá trị nhỏ nhất bằng -1.

Câu 47. Tập nghiệm của phương trình: 3^2x - (2^x + 9).3^x + 9.2^x = 0 là:

A. {0}

B. {0; 2}

C. {2}

D. Ø

Câu 48. Hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt phẳng (ABC) một góc bằng 60^o. Khoảng cách từ điểm I đến mặt phẳng (SAB) theo a là:

Câu 49. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số điểm y = x³ - 2(m -1)x² + (m -1)x có 3 chung phân biệt với trục hoành.

A. 1 < m < 2

B. m ≥ 2 hoặc m ≤ 1

C. m > 2 hoặc m < 1

D. m > 2

Câu 50. Bán kính mặt cầu (S) ngoại tiếp hình tứ diện đều ABCD cạnh a dài là: