Toán lớp 4 trang 91 - Bài 93: Ôn tập về phân số - SGK Cánh diều

Câu 1

a) Đã tô màu vào $\frac{3}{5}$hình nào?

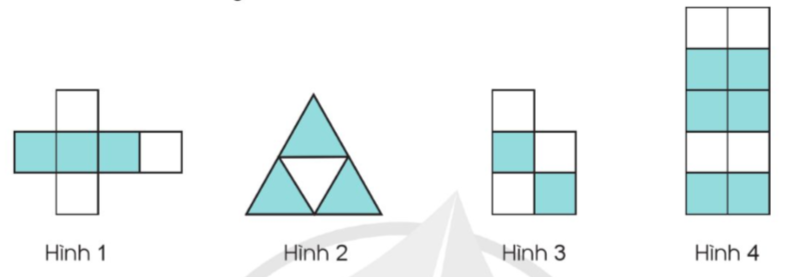
b) Phân số thứ nhất là $\frac{7}{8}$, phân số thứ hai là $\frac{3}{4}$. Hãy so sánh hai phân số đó. Tính tổng, hiệu, tích, thương của phân số thứ nhất và phân số thứ hai.

Phương pháp giải:

a) Phân số chỉ số phần được tô màu có tử số là số phần được tô màu, mẫu số là số phần bằng nhau.

b)

- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

- Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược

Lời giải chi tiết:

a) Ta thấy: Hình 4 được chia thành 10 phần bằng nhau, tô màu 6 phần.

Vậy đã tô màu $\frac{6}{{10}} = \frac{3}{5}$ hình 4.

b) So sánh hai phân số $\frac{7}{8}$ và $\frac{3}{5}$

Ta có: $\frac{7}{8} = \frac{{7 \times 5}}{{8 \times 5}} = \frac{{35}}{{40}}$   ;    $\frac{3}{5} = \frac{{3 \times 8}}{{5 \times 8}} = \frac{{24}}{{40}}$

Vì $\frac{{35}}{{40}} > \frac{{24}}{{40}}$ nên $\frac{7}{8}$> $\frac{3}{5}$

Thực hiện tính:

$\frac{7}{8} + \frac{3}{5} = \frac{{35}}{{40}} + \frac{{24}}{{40}} = \frac{{59}}{{40}}$

$\frac{7}{8} - \frac{3}{5} = \frac{{35}}{{40}} - \frac{{24}}{{40}} = \frac{{11}}{{40}}$

$\frac{7}{8} \times \frac{3}{5} = \frac{{7 \times 3}}{{8 \times 5}} = \frac{{21}}{{40}}$

$\frac{7}{8}:\frac{3}{5} = \frac{7}{8} \times \frac{5}{3} = \frac{{35}}{{24}}$

Câu 2

Tính:

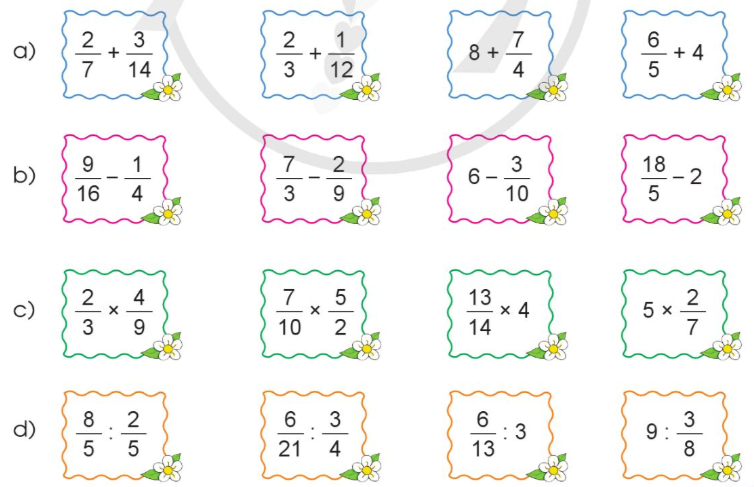
Phương pháp giải:

- Muốn cộng (hoặc trừ) hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng (hoặc trừ) hai phân số đó.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược

Lời giải chi tiết:

a) $\frac{2}{7} + \frac{3}{{14}} = \frac{4}{{14}} + \frac{3}{{14}} = \frac{7}{{14}} = \frac{1}{2}$

$\frac{2}{3} + \frac{1}{{12}} = \frac{8}{{12}} + \frac{1}{{12}} = \frac{9}{{12}} = \frac{3}{4}$

$8 + \frac{7}{4} = \frac{{32}}{4} + \frac{7}{4} = \frac{{39}}{4}$

$\frac{6}{5} + 4 = \frac{6}{5} + \frac{{20}}{5} = \frac{{26}}{5}$

b) $\frac{9}{{16}} - \frac{1}{4} = \frac{9}{{16}} - \frac{4}{{16}} = \frac{5}{{16}}$

$\frac{7}{3} - \frac{2}{9} = \frac{{21}}{9} - \frac{2}{9} = \frac{{19}}{9}$

$6 - \frac{3}{{10}} = \frac{{60}}{{10}} - \frac{3}{{10}} = \frac{{57}}{{10}}$

$\frac{{18}}{5} - 2 = \frac{{18}}{5} - \frac{{10}}{5} = \frac{8}{5}$

c) $\frac{2}{3} \times \frac{4}{9} = \frac{{2 \times 4}}{{3 \times 9}} = \frac{8}{{27}}$

$\frac{7}{{10}} \times \frac{5}{2} = \frac{{7 \times 5}}{{10 \times 2}} = \frac{{35}}{{20}} = \frac{7}{4}$

$\frac{{13}}{{14}} \times 4 = \frac{{13 \times 4}}{{14}} = \frac{{52}}{{14}} = \frac{{26}}{7}$

$5 \times \frac{2}{7} = \frac{{5 \times 2}}{7} = \frac{{10}}{7}$

d) $\frac{8}{5}:\frac{2}{5} = \frac{8}{5} \times \frac{5}{2} = 4$

$\frac{6}{{21}}:\frac{3}{4} = \frac{6}{{21}} \times \frac{4}{3} = \frac{{24}}{{63}} = \frac{8}{{21}}$

$\frac{6}{{13}}:3 = \frac{6}{{13}} \times \frac{1}{3} = \frac{6}{{39}} = \frac{2}{{13}}$

$9:\frac{3}{8} = 9 \times \frac{8}{3} = \frac{{72}}{3} = 24$

Câu 3

Tính:

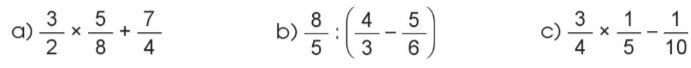
Phương pháp giải:

- Biểu thức có chứa phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau.

- Biểu thức có chứa dấu ngoặc thì ta thực hiện phép tính ở trong ngoặc trước

Lời giải chi tiết:

a) $\frac{3}{2} \times \frac{5}{8} + \frac{7}{4} = \frac{{15}}{{16}} + \frac{7}{4} = \frac{{15}}{{16}} + \frac{{28}}{{16}} = \frac{{43}}{{16}}$

b) $\frac{8}{5}:\left( {\frac{4}{3} - \frac{5}{6}} \right) = \frac{8}{5}:\left( {\frac{8}{6} - \frac{5}{6}} \right) = \frac{8}{5}:\frac{1}{2} = \frac{8}{5} \times 2 = \frac{{16}}{5}$

c) $\frac{3}{4} \times \frac{1}{5} - \frac{1}{{10}} = \frac{3}{{20}} - \frac{1}{{10}} = \frac{3}{{20}} - \frac{2}{{20}} = \frac{1}{{20}}$

Câu 4

Trong $\frac{1}{4}$giờ, con ốc sên thứ nhất bò được $\frac{2}{5}$m, con ốc sên thứ hai bò được 45 cm. Hỏi con ốc sên nào bò nhanh hơn?

Phương pháp giải:

Bước 1: Đổi $\frac{2}{5}$ mét sang mét

Bước 2: So sánh quãng đường hai con ốc sên bò được rồi kết luận

Lời giải chi tiết:

Đổi $\frac{2}{5}$m = 40 cm

Mà 40 cm < 45 cm, nên:

Vậy trong $\frac{1}{4}$giờ, con ốc sên thứ hai bò nhanh hơn con ốc sên thứ nhất.

Câu 5

Mẹ mua 24 kg bột mì, mẹ đã làm bánh hết $\frac{3}{8}$số bột mì đó. Hỏi:

a) Mẹ đã dùng hết bao nhiêu ki-lô-gam bột mì?

b) Mẹ còn lại bao nhiêu ki-lô-gam bột mì?

Phương pháp giải:

a) Số ki-lô-gam bột mì đã dùng hết = số kg bột mì mẹ mua x số phần bột mì mẹ đã làm bánh

b) Số ki-lô-gam bột mì còn lại = số kg bột mì mẹ mua – số ki-lô-gam bột mì đã dùng hết

Lời giải chi tiết:

Tóm tắt

Mua: 24 kg bột mì

Làm bánh: $\frac{3}{8}$số bột mì

a) Đã dùng: ? kg

b) Còn lại: ? kg

Bài giải

a) Mẹ đã dùng hết số ki-lô-gam bột mì là:

           $24 \times \frac{3}{8} = 9$(kg)

b) Mẹ còn lại số ki-lô-gam bột mì là:

            24 – 9 = 15 (kg)

             Đáp số: a) 9 kg bột mì

                          b) 15 kg bột mì

Câu 6

Một căn phòng hình vuông có diện tích 72 m². Bác Sáu định lát nền căn phòng bằng loại gạch hình vuông có cạnh $\frac{3}{5}m$. Em hãy tính xem bác Sáu cần phải mua bao nhiêu viên gạch để lát kín nền căn phòng đó, biết rằng phần mạch vữa không đáng kể.

Phương pháp giải:

Bước 1: Diện tích một viên gạch = cạnh x cạnh

Bước 2: Số viên gạch cần để lát kín nền = diện tích căn phòng : diện tích một viên gạch

Lời giải chi tiết:

Tóm tắt:

Căn phòng: 72 m²

Viên gạch hình vuông cạnh: $\frac{3}{5}m$

Số viên gạch: ? viên

Bài giải

Diện tích một viên gạch hình vuông là:

$\frac{3}{5} \times \frac{3}{5} = \frac{9}{{25}}$ (m²)

Số viên gạch để lát kín nền căn phòng là:

$72:\frac{9}{{25}} = 200$(viên)

Đáp số: 200 viên gạch