Toán lớp 4 trang 57 - Bài 78: Luyện tập - SGK Cánh diều
Báo gấm và lợn rừng cùng chạy. Khi lợn rừng chạy được 1/6 quãng đường. Nguyên liệu mẹ mua về làm bánh gồm có: 9/4 kg gạo nếp
Câu 1
Tính.
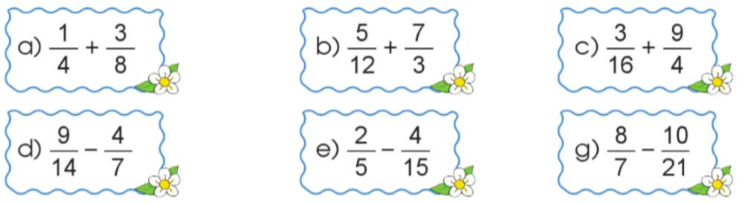
Phương pháp giải:
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{1}{4} + \frac{3}{8} = \frac{2}{8} + \frac{3}{8} = \frac{5}{8}$
b) $\frac{5}{{12}} + \frac{7}{3} = \frac{5}{{12}} + \frac{{28}}{{12}} = \frac{{33}}{{12}}$
c) $\frac{3}{{16}} + \frac{9}{4} = \frac{3}{{16}} + \frac{{36}}{{16}} = \frac{{39}}{{16}}$
d) $\frac{9}{{14}} - \frac{4}{7} = \frac{9}{{14}} - \frac{8}{{14}} = \frac{1}{{14}}$
e) $\frac{2}{5} - \frac{4}{{15}} = \frac{6}{{15}} - \frac{4}{{15}} = \frac{2}{{15}}$
g) $\frac{8}{7} - \frac{{10}}{{21}} = \frac{{24}}{{21}} - \frac{{10}}{{21}} = \frac{{14}}{{21}} = \frac{2}{3}$
Câu 2
Rút gọn rồi tính:
a) $\frac{8}{{18}} + \frac{5}{3}$
b) $\frac{8}{{24}} + \frac{4}{{48}}$
c) $\frac{{20}}{{15}} - \frac{4}{{45}}$
d) $\frac{{40}}{{32}} - \frac{1}{2}$
Phương pháp giải:
- Rút gọn các phân số thành phân số tối giản
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:
a) $\frac{8}{{18}} + \frac{5}{3} = \frac{4}{9} + \frac{5}{3} = \frac{4}{9} + \frac{{15}}{9} = \frac{{19}}{9}$
b) $\frac{8}{{24}} + \frac{4}{{48}} = \frac{1}{3} + \frac{1}{{12}} = \frac{4}{{12}} + \frac{1}{{12}} = \frac{5}{{12}}$
c) $\frac{{20}}{{15}} - \frac{4}{{45}} = \frac{4}{3} - \frac{4}{{45}} = \frac{{60}}{{45}} - \frac{4}{{45}} = \frac{{56}}{{45}}$
d) $\frac{{40}}{{32}} - \frac{1}{2} = \frac{5}{4} - \frac{1}{2} = \frac{5}{4} - \frac{2}{4} = \frac{3}{4}$
Câu 3
Tính (theo mẫu):
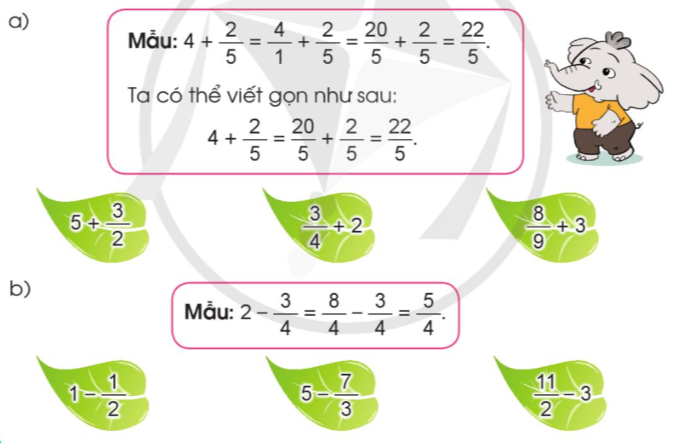
Phương pháp giải:
Ta có thể viết các số tự nhiên dưới dạng phân số, sau đó thực hiện phép cộng, phép trừ hai phân số như thông thường.
Lời giải chi tiết:
a) $5 + \frac{3}{2} = \frac{{10}}{2} + \frac{3}{2} = \frac{{13}}{2}$
$\frac{3}{4} + 2 = \frac{3}{4} + \frac{8}{4} = \frac{{11}}{4}$
$\frac{8}{9} + 3 = \frac{8}{9} + \frac{{27}}{9} = \frac{{35}}{9}$
b) $1 - \frac{1}{2} = \frac{2}{2} - \frac{1}{2} = \frac{1}{2}$
$5 - \frac{7}{3} = \frac{{15}}{3} - \frac{7}{3} = \frac{8}{3}$
$\frac{{11}}{2} - 3 = \frac{{11}}{2} - \frac{6}{2} = \frac{5}{2}$
Câu 4
Chọn đáp án đúng:
Báo gấm và lợn rừng cùng chạy. Khi lợn rừng chạy được $\frac{1}{6}$quãng đường thì báo gấm chạy được $\frac{1}{2}$quãng đường đó. Hỏi báo gấm chạy nhanh hơn lợn rừng bao nhiêu phần quãng đường?
A. $\frac{2}{3}$
B.$\frac{2}{8}$
C.$\frac{5}{6}$
D.$\frac{1}{3}$
Phương pháp giải:
Số phần quãng đường báo gấm chạy nhanh hơn lợn rừng = số phần quãng đường báo gấm chạy được – số phần quãng đường lợn rừng chạy được
Lời giải chi tiết:
Quãng đường báo gấm chạy nhanh hơn lợn rừng là: $\frac{1}{2} - \frac{1}{6} = \frac{1}{3}$ (quãng đường)
Chọn D.
Câu 5
Nguyên liệu mẹ mua về làm bánh gồm có: $\frac{9}{4}$kg gạo nếp, $\frac{1}{2}$kg đỗ xanh, $\frac{3}{4}$kg thịt. Hỏi mẹ đã mua tất cả bao nhiêu ki-lô-gam nguyên liệu?

Phương pháp giải:
Số ki-lô-gam nguyên liệu mẹ đã mua = số kg gạo nếp + số kg đỗ xanh + số kg thịt
Lời giải chi tiết:
Số ki-lô-gam nguyên liệu mẹ đã mua là:
$\frac{9}{4} + \frac{1}{2} + \frac{3}{4} = \frac{7}{2}$ (kg)
Đáp số: $\frac{7}{2}$kg nguyên liệu
Câu 6
Hãy giúp bạn Voi tìm được vườn mía bằng cách thực hiện đúng các phép cộng, phép trừ hai phân số trên đường đi:
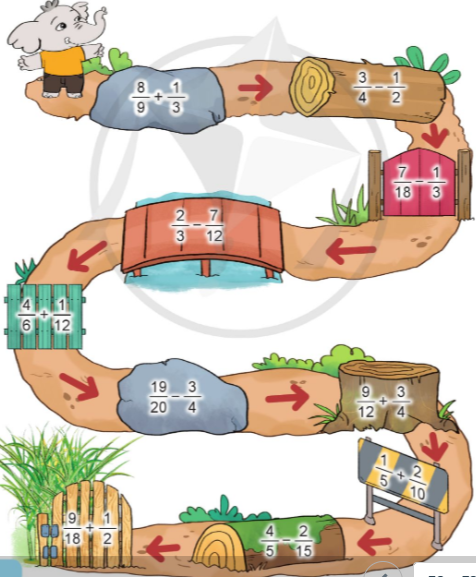
Phương pháp giải:
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
- Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số của hai phân số, rồi trừ hai phân số đó.
Lời giải chi tiết:

Search google: "từ khóa + timdapan.com" Ví dụ: "Toán lớp 4 trang 57 - Bài 78: Luyện tập - SGK Cánh diều timdapan.com"







