Bài 2 : Ôn tập : Tính chất cơ bản của phân số
Giải bài tập 1, 2, 3 trang 4 VBT toán 5 bài 2 : Ôn tập : Tính chất cơ bản của phân số với lời giải chi tiết và cách giải nhanh, ngắn nhất
Bài 1
Rút gọn các phân số
\(\eqalign{
& {{18} \over {30}} = .....\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{36} \over {27}} = .....\cr
& {{64} \over {80}} = .....\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{45} \over {35}} = ..... \cr} \)
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
\(\displaystyle {{18} \over {30}} = {18:6 \over 30:5} = {3 \over 5}\) ; \(\displaystyle {{36} \over {27}} ={{36:9} \over {27:9}}= {4 \over 3}\) ;
\(\displaystyle{{64} \over {80}} ={{64:8} \over {80:8}}={{8} \over {10}}={{8:2} \over {10:2}}= {4 \over 5}\) ;
\(\displaystyle {{45} \over {35}} ={{45:5} \over {35:5}}= {9 \over 7} \)
Bài 2
Quy đồng mẫu số hai phân số
a) \( \displaystyle {4 \over 5} \) và \( \displaystyle {7 \over 9} \) ; \( \displaystyle;MSC = .....\;;\;{4 \over 5} = .....;{7 \over 9} = .....\)
b) \( \displaystyle {5 \over 6}\) và \( \displaystyle {{17} \over {18}}\)
c) \( \displaystyle {3 \over 8}\) và \( \displaystyle {7 \over {12}}\)
Lưu ý: MSC là viết tắt của “Mẫu số chung”.
Phương pháp giải:
Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) \( \displaystyle {4 \over 5} \) và \( \displaystyle {7 \over 9} \)
MSC: \(45\) ;
\( \displaystyle {4 \over 5} = {{4 \times 9} \over {5 \times 9}} = {{36} \over {45}}\;\;;\;\;\;\quad \) \( \displaystyle{7 \over 9} = {{7 \times 5} \over {9 \times 5}} = {{35} \over {45}}.\)
b) \( \displaystyle {5 \over 6}\) và \( \displaystyle {{17} \over {18}}\)
MSC: \(18\) ;
\( \displaystyle {5 \over 6} = {{5 \times 3} \over {6 \times 3}} = {{15} \over {18}}\) ; Giữ nguyên phân số \(\displaystyle {{17} \over {18}}.\)
c) \( \displaystyle {3 \over 8}\) và \( \displaystyle {7 \over {12}}\)
MSC: \(24\) ;
\( \displaystyle {3 \over 8} = {{3 \times 3} \over {8 \times 3}} = {9 \over {24}}\;\;;\;\;\;\quad\) \( \displaystyle{7 \over {12}} = {{7 \times 2} \over {12 \times 2}} = {{14} \over {24}}\)
Bài 3
a) Nối với phân số bằng \(\displaystyle {2 \over 5}\) (theo mẫu) :
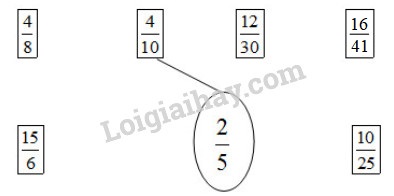
b) Nối với phân số bằng \(\displaystyle {{12} \over {18}}\) (theo mẫu) :
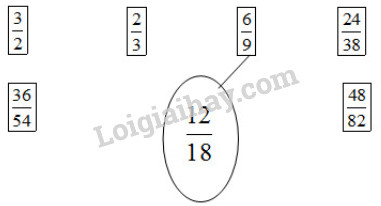
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số :
- Nếu nhân cả tử và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
a) Ta có :
\(\dfrac{2}{5} =\dfrac{2\times 2}{5 \times 2} = \dfrac{4}{10} \) ; \(\dfrac{2}{5} =\dfrac{2\times 6}{5 \times 6} = \dfrac{12}{30} \).
\(\dfrac{2}{5} =\dfrac{2\times 5}{5 \times 5} = \dfrac{10}{25} \)
Vậy ta có kết quả như sau :
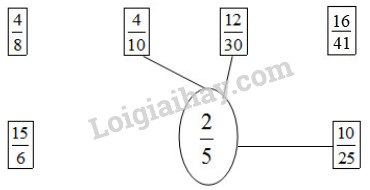
b) Ta có :
\(\dfrac{12}{18} =\dfrac{12:6}{18:6} = \dfrac{2}{3} \) ; \(\dfrac{12}{18} =\dfrac{12:2}{18:2} = \dfrac{6}{9} \)
\(\dfrac{12}{18} =\dfrac{12\times 3}{18 \times 3} = \dfrac{36}{54} \).
Vậy ta có kết quả như sau :
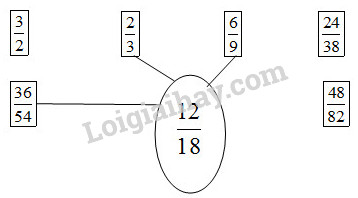
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2 : Ôn tập : Tính chất cơ bản của phân số timdapan.com"







