Giải mục 2 trang 18, 19 SGK Toán 11 tập 2 - Kết nối tri thức

Hoạt động 3

a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?

b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?

Phương pháp giải:

Thay các giá trị x lần lượt để tính y.

Lời giải chi tiết:

a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)

Với \(x = 2\) thì \(y = {\log _2}2 = 1\)

Với \(x = 4\) thì \(y = {\log _2}4 = 2\)

b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.

Câu hỏi 2

Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.

a) \(y = {\log _{\sqrt 3 }}x;\)   

b) \(y = {\log _{{2^{ - 2}}}}x;\) 

c) \(y = {\log _x}2;\)            

d) \(y = {\log _{\frac{1}{x}}}5.\)

Phương pháp giải:

Sử dụng định nghĩa hàm số lôgarit

Lời giải chi tiết:

a) \(y = {\log _{\sqrt 3 }}x\) là hàm số lôgarit có cơ số \(\sqrt 3 .\)

b) \(y = {\log _{{2^{ - 2}}}}x;\) là hàm số lôgarit có cơ số \({2^{ - 2}} = \frac{1}{4}.\)    

c) \(y = {\log _x}2\) không là hàm số lôgarit.

d) \(y = {\log _{\frac{1}{x}}}5\) không hàm số lôgarit.

Hoạt động 4

Cho hàm số lôgarit \(y = {\log _2}x.\)

a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số \(y = {\log _2}x\)

c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số \(y = {\log _2}x\)

Phương pháp giải:

Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.

Lời giải chi tiết:

a) Lập bảng giá trị của hàm số tại một điểm như sau:

b, 

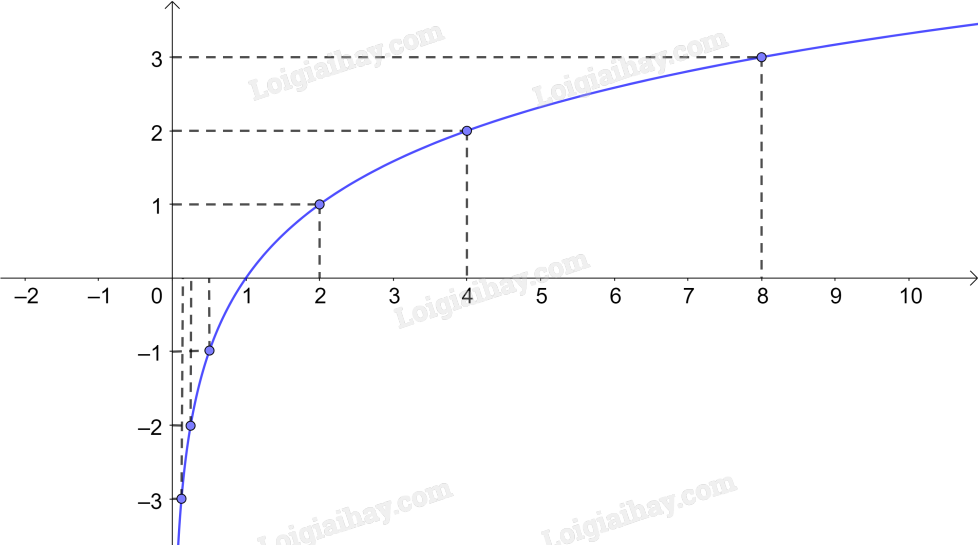
c) Tập giá trị: \(\mathbb{R}\)

Tính chất biến thiên: đồng biến

Vận dụng

Giải bài toán tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).

Phương pháp giải:

Sử dụng công thức tăng trưởng mũ: \(A = P{e^{rt}}\)

Lời giải chi tiết:

Từ năm 2020 đến năm 2050 là 30 năm.

Ước tính dân số Việt Nam vào năm 2050 là: \(97,34.{e^{0,91\% .30}} = 127,8950498\)(triệu người)