Giải đề thi học kì 1 toán lớp 7 năm 2020 - 2021 tỉnh Bạc Liêu

Câu 1 (2,0 điểm). Thực hiện phép tính:

a) \(\frac{5}{4} + \frac{7}{4}\)

b) \(\frac{7}{9}.33\frac{1}{5} - \frac{7}{9}.6\frac{1}{5}\)

Câu 2 (2,0 điểm).

a) Tìm x biết \(x + \frac{5}{6} = \frac{{ - 1}}{2}.\)

b) Tìm hai số a, b biết \(\frac{a}{8} = \frac{b}{9}\) và \(a + b = 34\).

Câu 3 (2,0 điểm).

a) Cho hàm số \(y = f\left( x \right) = 2x + 1.\) Tính \(f\left( 0 \right);\,\,f\left( {\frac{1}{2}} \right)\).

Câu 4 (2,0 điểm).

a) Cho tam giác ABC có \(\widehat A = {85^0},\,\,\,\widehat B = {45^0}\). Tính số đo của góc C.

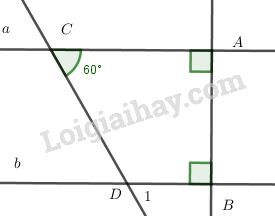
b) Cho hình vẽ. Vì sao a//b? Tính \(\widehat {{D_1}}\)?

Câu 5 (2,0 điểm). Cho tam giác ABC có AB<AC. Gọi D là trung điểm của AC. Trên tia đối của tia DB lấy điểm M sao cho DM = DB.

a) Chứng mình \(\Delta ADB = \Delta CMD\).

b) Trên tia đối của tia CM lấy điểm E sao cho CE = CM. Chứng minh BE//AC.

LỜI GIẢI CHI TIẾT

Câu 1:

a) \(\frac{5}{4} + \frac{7}{4} = \frac{{5 + 7}}{4} = \frac{{12}}{4} = 3\)

b)

\(\begin{array}{l}\frac{7}{9}.33\frac{1}{5} - \frac{7}{9}.6\frac{1}{5} = \frac{7}{9}.\left( {33\frac{1}{5} - 6\frac{1}{5}} \right)\\ = \frac{7}{9}.27 = 21\end{array}\)

Câu 2:

a)

\(\begin{array}{l}x + \frac{5}{6} = \frac{{ - 1}}{2}\\x = \frac{{ - 1}}{2} - \frac{5}{6}\\x = \frac{{ - 3}}{6} - \frac{5}{6}\\x = \frac{{ - 8}}{6}\\x = \frac{{ - 4}}{3}\end{array}\)

Vậy \(x = \frac{{ - 4}}{3}\).

b) Áp dụng tính chất dãy tỉ số bằng nhay ta có:

\(\frac{a}{8} = \frac{b}{9} = \frac{{a + b}}{{8 + 9}} = \frac{{34}}{{17}} = 2\)

+) \(\frac{a}{8} = 2 \Rightarrow a = 2.8 = 16\)

+) \(\frac{b}{9} = 2 \Rightarrow b = 2.9 = 18\)

Vậy a=16 và b=18

Câu 3:

a) \(f\left( 0 \right) = 2.0 + 1 = 1\)

\(f\left( {\frac{1}{2}} \right) = 2.\frac{1}{2} + 1 = 2\)

b) Vì số máy x tỉ lệ thuận với số lít xăng y tiêu thụ nên ta có y = kx  (1)

Khi x=8 thì y=70 thay vào (1) ta có 70 = k.8 => k = 8,75

Suy ra ta có: y = 8,75x (2)

Thay x = 13 vào (2) ta được: y = 8,75. 13 = 113,75 (lít)

Vậy dùng 13 máy thì tiêu thụ hết 113,75 lít xăng

Câu 4:

a) Xét tam giác ABC có:

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow {85^0} + {45^0} + \widehat C = {180^0}\\ \Rightarrow \widehat C = {180^0} - {85^0} - {45^0}\\ \Rightarrow \widehat C = {50^0}\end{array}\)

Vậy \(\widehat C = {50^0}\)

b) Ta có:

\(\)\(\left. \begin{array}{l}a \bot AB\\b \bot AB\end{array} \right\} \Rightarrow a//b\)

Vì a//b nên ta có : \(\widehat {C} + \widehat {CDB}=180^0\)

Mà  \(\widehat {CDB} + \widehat {D_1}=180^0 (2 góc kề bù)\) nên \( \widehat {D_1} = \widehat {C} =60^0\) 

Câu 5:

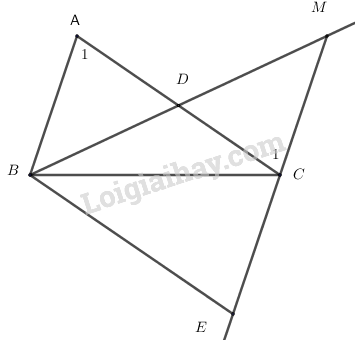
a) Xét \(\Delta ABD\) và \(\Delta CMD\) có:

AD = DC (D là trung điểm của AC)

\(\widehat {ADB} = \widehat {CMD}\) (đối đỉnh)

DB = DM (gt)

\( \Rightarrow \,\,\Delta ABD = \Delta CMD\) (c.g.c)

b) Do \(\,\Delta ABD = \Delta CMD\) nên \(\widehat {{A_1}} = \widehat {{C_1}}\) (2 góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AB//MC hay AB//CE

Cũng từ \(\,\Delta ABD = \Delta CMD\) ta có AB = CM (2 cạnh tương ứng)

Mà CM = CE (gt) nên AB = CE

Xét \(\Delta ABC\) và \(\Delta ECB\) có:

AB = CE

\(\widehat {ABC} = \widehat {ECB}\) (so le trong)

BC chung

=> \(\Delta ABC\) =  \(\Delta ECB\) (c.g.c)

\( \Rightarrow \widehat {ACB} = \widehat {EBC}\) (2 góc tương ứng)

 Mà hai góc này ở vị trí so le trong nên AC//BE (đpcm).