Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Hóc Môn

Bài 1 (2,5 điểm):Thực hiện phép tính

\(a)\,\,3,5 - \left( {\dfrac{{ - 2}}{7}} \right)\)              \(b)\,\,\dfrac{{{2^{15}}{{.9}^3}}}{{{6^3}{{.8}^3}}}\)                        \(c)\,\,{\left( {\dfrac{1}{2}} \right)^2} + \left| {\dfrac{{ - 3}}{4}} \right| - \dfrac{{\sqrt {81} }}{{16}}\)

Bài 2 (1,5 điểm): Tìm số tự nhiên \(x\), biết:

\(a)\,\,\dfrac{1}{3} + x = \dfrac{3}{4}\)                                 \(b)\,\,{\left( {x - 5} \right)^2} = \dfrac{{49}}{4}\)

Bài 3 (1,0 điểm): Tìm \(x\) và \(y\) biết: \(\dfrac{x}{5} = \dfrac{y}{7}\) và \(x + 2y = 57.\)

Bài 4 (1,0 điểm): Cho hàm số \(y = f\left( x \right) = 3x - 1\).

a) Tính \(f\left( {\dfrac{{ - 1}}{3}} \right)\,;\,\,\,\,f\left( 0 \right)\).

b) Tìm \(x\) khi \(y =  - 1\).

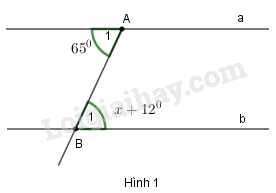
Bài 5 (1,0 điểm): Hình 1 cho biết \(a//b\) và \(\widehat {{A_1}} = 65^\circ ,\,\,\widehat {{B_1}} = x + 12^\circ \). Hãy tìm \(x\)

Bài 6 (1,0 điểm): Trong dịp nghỉ hè vừa qua, An, Phúc, Thịnh cùng đi câu cá, An câu được \(8\) con, Phúc câu được \(12\) con, Thịnh câu được \(10\) con. Ba bạn mang ra chợ bán được tổng số tiền là \(180\) nghìn đồng và quyết định chia tiền tỉ lệ với số cá câu được của mỗi bạn. Hỏi mỗi bạn được bao nhiêu tiền?

Bài 7 (2,0 điểm): Cho tam giác \(ABC\)có \(3\)  góc nhọn. Kẻ \(AK\) vuông góc với \(BC\)(\(K\) thuộc \(BC\)). Trên tia đối của tia \(KA\) lấy điểm \(D\) sao cho \(KD = KA\).

a) Chứng minh \(\Delta AKB = \Delta DKB\).

b) Chứng minh \(CB\) là phân giác của \(\widehat {ACD}\).

c) Gọi \(H\) là trung điểm của \(BC\). Trên tia \(AH\) lấy điểm \(E\) sao cho \(H\) là trung điểm của \(AE\). Chứng minh \(CE = BD\).

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Bài 1 (VD):

Phương pháp:

a) c) - Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

                        Lũy thừa \( \to \) Nhân và chia \( \to \) Cộng và trừ

- Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc:

                        \((\,\,)\,\, \to {\rm{[}}\,\,{\rm{]}}\,\, \to {\rm{\{ }}\,\,{\rm{\} }}\)

b)  Sử dụng: \({\left( {a.b} \right)^m} = {a^m}{b^m};\,{\left( {\dfrac{a}{b}} \right)^m} = \dfrac{{{a^m}}}{{{b^m}}};\,\)\({a^m}:{a^n} = {a^{m - n}}\)

Cách giải:

\(a)\,\,3,5 - \left( {\dfrac{{ - 2}}{7}} \right) = \dfrac{7}{2} + \dfrac{2}{7}\)\( = \dfrac{{49}}{{14}} + \dfrac{4}{{14}} = \dfrac{{53}}{{14}}\)

\(b)\,\,\dfrac{{{2^{15}}{{.9}^3}}}{{{6^3}{{.8}^3}}} = \dfrac{{{2^{15}}.{{\left( {3.3} \right)}^3}}}{{{{\left( {2.3} \right)}^3}.{{\left( {{2^3}} \right)}^3}}}\)\(\dfrac{{{2^{15}}{{.3}^3}{{.3}^3}}}{{{2^3}{{.3}^3}{{.2}^9}}} = \dfrac{{{2^{15}}{{.3}^3}}}{{{2^{12}}}} = \dfrac{{{2^{12}}{{.2}^3}{{.3}^3}}}{{{2^{12}}}}\)\( = {2^3}{.3^3} = {6^3} = 216\)

\(c)\,\,{\left( {\dfrac{1}{2}} \right)^2} + \left| {\dfrac{{ - 3}}{4}} \right| - \dfrac{{\sqrt {81} }}{{16}}\)\( = \dfrac{1}{4} + \dfrac{3}{4} - \dfrac{9}{{16}}= \dfrac{4}{4} - \dfrac{9}{{16}}\)\(  = \dfrac{{16}}{{16}} - \dfrac{9}{{16}} = \dfrac{7}{{16}}\)

Bài 2 (VD):

Phương pháp:

- Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.

- Áp dụng tính chất : \({A^2} = {B^2}\, \Rightarrow A = B\) hoặc \(A =  - B\).

Cách giải:

\(\begin{array}{l}a)\,\,\dfrac{1}{3} + x = \dfrac{3}{4}\\\,\,\,\,\,\,x = \dfrac{3}{4} - \dfrac{1}{3}\\\,\,\,\,\,\,x = \dfrac{5}{{12}}\end{array}\)

Vậy \(x = \dfrac{5}{{12}}.\)

\(\begin{array}{l}b)\,\,{\left( {x - 5} \right)^2} = \dfrac{{49}}{4}\\\,\,\,\,\,\,{\left( {x - 5} \right)^2} = {\left( {\dfrac{7}{2}} \right)^2}\end{array}\)

\( \Rightarrow \left[ \begin{array}{l}x - 5 = \dfrac{7}{2}\\x - 5 = \dfrac{{ - 7}}{2}\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}x = \dfrac{7}{2} + 5\\x = \dfrac{{ - 7}}{2} + 5\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}x = \dfrac{{17}}{2}\\x = \dfrac{3}{2}\end{array} \right.\)

Vậy \(x = \dfrac{{17}}{2}\) hoặc \(x = \dfrac{3}{2}.\)

Bài 3 (VD):

Phương pháp:

Áp dụng tính chất dãy tỉ số bằng nhau:

Từ dãy tỉ số bằng nhau \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f}\) ta suy ra: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c - e}}{{b + d - f}}\).

Cách giải:

\(\dfrac{x}{5} = \dfrac{y}{7}\) và \(x + 2y = 57\)

Ta có \(\dfrac{x}{5} = \dfrac{y}{7}\,\, \Rightarrow \,\,\dfrac{x}{5} = \dfrac{{2y}}{{14}}\,\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\,\dfrac{x}{5} = \dfrac{{2y}}{{14}}\, = \dfrac{{x + 2y}}{{5 + 14}} = \dfrac{{57}}{{19}} = 3\\\dfrac{x}{5} = 3\,\Rightarrow x = 3.5 = 15\\\dfrac{{2y}}{{14}} = 3\Rightarrow 2y = 42 \Rightarrow y = 42:2 = 21\end{array}\)

Vậy \(x = 15\) và \(y = 21\).

Bài 4 (VD):

Phương pháp:

a) Thay các giá trị \(x = \dfrac{{ - 1}}{3};\,x = 0\) vào \(f(x)\) rồi tính giá trị tương ứng của \(y\).

b) Thay giá trị của \(y\) vào biểu thức rồi tìm giá trị tương ứng của \(x\).

Cách giải:

Cho hàm số \(y = f\left( x \right) = 3x - 1\).

a) Tính \(f\left( {\dfrac{{ - 1}}{3}} \right)\,;\,\,\,\,f\left( 0 \right)\).

Với \(x = \dfrac{{ - 1}}{3}\) ta có \(y = f\left( {\dfrac{{ - 1}}{3}} \right) = 3.\dfrac{{ - 1}}{3} - 1 \)\(=  - 1 - 1 =  - 2\).

Với \(x = 0\) ta có \(y = f\left( 0 \right) = 3.0 - 1 =  - 1\)

Vậy \(f\left( {\dfrac{{ - 1}}{3}} \right) =  - 2\,;\,\,\,\,f\left( 0 \right) =  - 1.\)

b) Tìm \(x\) khi \(y =  - 1\).

Với \(y =  - 1\) ta có:  \( - 1 = 3x - 1 \Rightarrow 3x = 0 \Rightarrow x = 0\)

Vậy khi \(y =  - 1\) thì \(x = 0\).

Bài 5 (VD):

Phương pháp:

Áp dụng tính chất: Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau và hai góc trong cùng phía bù nhau.

Cách giải:

Vì \(a//b\) nên \(\widehat {{A_1}} = \,\,\widehat {{B_1}}\) (hai góc so le trong)

\(\begin{array}{l} \Rightarrow 65^\circ  = x + 12^\circ \\ \Rightarrow x = 65^\circ  - 12^\circ  = 53^\circ \end{array}\)

Vậy \(x = 53^\circ \).

Bài 6 (VD):

Phương pháp:

Áp dụng tính chất dãy tỉ số bằng nhau: Từ dãy tỉ số bằng nhau \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f}\) ta suy ra: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c - e}}{{b + d - f}}\).

Cách giải:

Gọi số tiền An, Phúc, Thịnh nhận được lần lượt là \(x\,;\,\,y\,;\,\,z\,\)(nghìn đồng) \((x,y,z \in \mathbb{N}*)\).

Theo bài ra ta có: \(\dfrac{x}{8} = \dfrac{y}{{12}} = \dfrac{z}{{10}}\) và \(x + y + z = 180\).

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{8} = \dfrac{y}{{12}} = \dfrac{z}{{10}} = \dfrac{{x + y + z}}{{8 + 12 + 10}} \)\(= \dfrac{{180}}{{30}} = 6\)

\(\dfrac{x}{8} = 6 \Rightarrow x = 48\,\,\,(tm)\)

\(\dfrac{y}{{12}} = 6 \Rightarrow y = 72\,\,\,(tm)\)

\(\dfrac{z}{{10}} = 6 \Rightarrow z = 60\,\,\,(tm)\)

Vậy An nhận được \(48\) nghìn đồng, Phúc nhận được \(72\) nghìn đồng và Thịnh nhận được \(60\) nghìn đồng.

Bài 7 (VD):

Phương pháp:

- Áp dụng các trường hợp bằng nhau của tam giác và các tính chất của hai tam giác bằng nhau.

Cách giải:

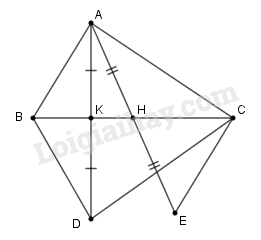
a) Chứng minh \(\Delta AKB = \Delta DKB\).

Xét hai tam giác vuông \(AKB\) và \(DKB\) ta có:

\(\widehat {AKB} = \widehat {DKB} = 90^\circ \) (vì \(AK \bot BC\) tại \(K\))

Cạnh \(BK\) chung

\(KA = KD\,\,(gt)\)

Vậy \(\Delta AKB = \Delta DKB\,\,\left( {c.g.c} \right)\)

b) Chứng minh \(CB\) là phân giác của \(\widehat {ACD}\).

Ta có  \(\Delta AKB = \Delta DKB\,\,\left( {c.g.c} \right)\)

\( \Rightarrow BA = BD\) (2 cạnh tương ứng)

và \(\widehat {ABK} = \widehat {DBK}\) (2 góc tương ứng)

Xét \(\Delta ACB\) và \(\Delta DCB\) có:

\(BA = BD\,\,\left( {cmt} \right)\)

\(\widehat {ABC} = \widehat {DBC}\)

Cạnh \(BC\) chung

Vậy \(\Delta ACB = \Delta DCB\,\,\left( {c.g.c} \right)\)

\( \Rightarrow \widehat {ACB} = \widehat {DCB}\) (hai góc tương ứng)

\( \Rightarrow CB\) là phân giác của \(\widehat {ACD}\).

c) Gọi \(H\) là trung điểm của \(BC\). Trên tia \(AH\) lấy điểm \(E\) sao cho \(H\) là trung điểm của \(AE\). Chứng minh \(CE = BD\).

Xét \(\Delta AHB\) và \(\Delta EHC\) có:

\(AH = HE\,\left( {gt} \right)\)

\(\widehat {AHB} = \widehat {EHC}\)(2 góc đối đỉnh)

\(HB = HC\,\,\left( {gt} \right)\)

Vậy \(\Delta AHB = \Delta EHC\,\,\left( {c.g.c} \right)\)

\( \Rightarrow AB = EC\) (hai cạnh tương ứng)

Lại có \(BA = BD\,\,\left( {cmt} \right)\).

Do đó \(CE = BD = AB\)

Vậy \(CE = BD\).

HẾT