Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 phòng GDĐT Phú Nhuận

Bài 1  (2,5 điểm): Thực hiện phép tính :

a) \(\dfrac{4}{7} - \dfrac{1}{{14}} + \dfrac{5}{{21}}\)

b) \({\left( {\dfrac{{ - 1}}{3}} \right)^3} \cdot \sqrt {{{\left( { - 3} \right)}^2}}  - \left| {\dfrac{{ - 4}}{3}} \right| + {2019^0}\)

c) \(\dfrac{{{3^{2019}}{{.4}^{20}}}}{{{6^{40}}{{.3}^{1980}}}}\)

Bài 2 (2,5 điểm): Tìm \(x\) biết :

a) \(\dfrac{2}{3}x + \dfrac{2}{3} =  - 1,5\)

b) \(\dfrac{1}{4} + \left| {\dfrac{x}{4}} \right| = \left| { - 10} \right|\)

c) \({3^{x + 1}} - {3^x} = 18\)

Bài 3 (1 điểm): Một thầy giáo thể dục mang một số tiền dự định mua \(4\) quả bóng đá về cho học sinh luyện tập năng khiếu thể thao. Do có đợt giảm giá, nên với cùng số tiền đó thầy đã mua được \(5\) quả với giá đã giảm là \(80\,000\) đồng một quả. Tính giá tiền ban đầu khi chưa giảm giá của một quả bóng đá.

Bài 4 (1 điểm): Hưởng ứng phong trào “Vì môi trường xanh”, trong năm học 2019 – 2020, tất cả trường học trên địa bàn TP.HCM phải xây dựng nhà trường đạt yêu cầu : “Văn minh, an toàn và xanh-sạch-đẹp”. thực hiện lớp học không rác, trường học không rác và lễ hội không rác. Tại một trường THCS, có \(4kg\) rác thải được phân thành \(3\) loại : rác tái chế, rác không tái chế, chất thải nguy hại lần lượt tỉ lệ với \(4,\,3,\,1.\) Tính số gam rác thải mỗi loại.

Bài 5 (0,5 điểm): Cho biết \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{a},\) với \(a,b,c\) là các số thực khác \(0.\) Tính giá trị của biểu thức : \(M = \dfrac{{{a^{2019}} + {b^{2019}} + {c^{2019}}}}{{{a^{672}}{b^{673}}{c^{674}}}} \cdot \)

Bài 6 (2,5 điểm): Cho tam giác \(ABC\) có \(AB = AC\) và \(AB > BC.\) Gọi \(M\) là trung điểm của cạnh \(BC.\)

a) Chứng minh \(\Delta ABM = \Delta ACM\) và \(AM \bot BC.\)

b) Trên cạnh \(AB\) lấy điểm \(D,\) trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AD = AE.\) Chứng minh \(MD = ME.\)

c) Gọi \(N\) là trung điểm của đoạn thẳng \(BD.\) Trên tia đối của tia \(NM\) lấy điểm \(K\) sao cho \(NK = NM.\) Chứng minh các điểm \(K,D,E\) thẳng hàng.

 

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

 

Bài 1 (VD):

Phương pháp:

a) Quy đồng mẫu rồi thực hiện các phép tính.

b) Chú ý kiến thức về căn bậc hai và \(\left| x \right| = \left[ \begin{array}{l}x\,khi\,x \ge 0\\ - x\,khi\,x < 0\end{array} \right.\) và \({a^0} = 1.\)

c) Vận dụng kiến thức : \({\left( {{a^m}} \right)^n} = {a^{m.n}};\,\dfrac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\) 

Cách giải:

a) \(\dfrac{4}{7} - \dfrac{1}{{14}} + \dfrac{5}{{21}} = \dfrac{7}{{14}} + \dfrac{5}{{21}} \)\(= \dfrac{{21 + 10}}{{42}} = \dfrac{{31}}{{42}}\)

b) \({\left( {\dfrac{{ - 1}}{3}} \right)^3} \cdot \sqrt {{{\left( { - 3} \right)}^2}}  - \left| {\dfrac{{ - 4}}{3}} \right| + {2019^0}\)

\(\begin{array}{l} = \dfrac{{ - 1}}{{27}} \cdot \sqrt 9  - \dfrac{4}{3} + 1\\ = \dfrac{{ - 1}}{{27}} \cdot 3 - \dfrac{4}{3} + 1\\ = \dfrac{{ - 1}}{9} - \dfrac{4}{3} + 1\\ = \dfrac{{ - 13}}{9} + 1\\ = \dfrac{{ - 4}}{9}\end{array}\)

c) \(\dfrac{{{3^{2019}}{{.4}^{20}}}}{{{6^{40}}{{.3}^{1980}}}} = \dfrac{{{3^{2019}}{{.2}^{40}}}}{{{2^{40}}{{.3}^{40}}{{.3}^{1980}}}} \)\(= \dfrac{{{3^{2019}}}}{{{3^{2020}}}} = \dfrac{1}{3}\)

Bài 2 (VD):

Phương pháp:

Áp dụng các quy tắc chuyển vế đổi dấu và kiến thức về giá trị tuyệt đối để tìm \(x\).

Lưu ý: \(\left| A \right| = m\,\,\left( {m \ge 0} \right)\) thì \(A = m\) hoặc \(A =  - m.\)

\({a^m} = {a^n}\,\left( {a > 0;a \ne 1} \right) \Rightarrow m = n\)

Cách giải:

a) \(\dfrac{2}{3}x + \dfrac{2}{3} =  - 1,5\)

\(\begin{array}{l}\dfrac{2}{3}x =  - 1,5 - \dfrac{2}{3}\\\dfrac{2}{3}x = \dfrac{{ - 13}}{6}\\x = \dfrac{{ - 13}}{6}:\dfrac{2}{3}\\x = \dfrac{{ - 13}}{4}\end{array}\)

Vậy \(x = \dfrac{{ - 13}}{4}.\)

b) \(\dfrac{1}{4} + \left| {\dfrac{x}{4}} \right| = \left| { - 10} \right|\)

\(\begin{array}{l}\left| {\dfrac{x}{4}} \right| = 10 - \dfrac{1}{4}\\\left| {\dfrac{x}{4}} \right| = \dfrac{{39}}{4}\end{array}\)

TH 1 :

\(\begin{array}{l}\dfrac{x}{4} = \dfrac{{39}}{4}\\x = 39\end{array}\)

TH2 :

\(\begin{array}{l}\dfrac{{ - x}}{4} = \dfrac{{39}}{4}\\x =  - 39\end{array}\)

Vậy \(x = 39;x =  - 39.\)

c) \({3^{x + 1}} - {3^x} = 18\)

\(\begin{array}{l}{3^x}.3 - {3^x} = 18\\{3^x}.\left( {3 - 1} \right) = 18\\{3^x}.2 = 18\\{3^x} = 18:2\\{3^x} = 9\\{3^x} = {3^2}\\x = 2\end{array}\)

Vậy \(x=2.\)

Bài 3 (VD):

Phương pháp:

- Tìm số tiền của 5 quả bóng khi mua với giá đã giảm.

- Tính giá tiền của một quả bóng lúc ban đầu.

Cách giải:

Thầy giáo mang theo số tiền dự định mua bóng là :

\(80\,000 \times 5 = 400\,000\) (đồng)

Giá tiền ban đầu khi chưa giảm của một quả bóng đá là :

\(400\,000:4 = 100\,000\) (đồng)

Đáp số : \(100\,000\) đồng.

Bài 4 (VD):

Phương pháp:

- Viết các tỉ lệ thức về khối lượng chất thải trong trường học với các tỉ lệ đã cho.

- Áp dụng tính chất dãy tỉ số bằng nhau, tính giá trị khối lượng của từng loại rác thải.

Cách giải:

Đổi : \(4kg = 4000g\)

Gọi \(x,y,z\) lần lượt là khối lượng của rác tái chế, rác không tái chế và chất thải nguy hại của trường THCS đó. \(\left( {gam,\,\,0 < x;y;z < 4000} \right)\)

Do khối lượng rác dược phân loại bằng \(4000g\) nên \(x + y + z = 4000\)

Mà khối lượng của ba loại rác sau khi phân loại lần lượt tỉ lệ với \(4,3,1\) nên ta có :

\(\dfrac{x}{4} = \dfrac{y}{3} = \dfrac{z}{1}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{x}{4} = \dfrac{y}{3} = \dfrac{z}{1} = \dfrac{{x + y + z}}{{4 + 3 + 1}} \)\(= \dfrac{{4000}}{8} = 500\)

\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{x}{4} = 500 \Rightarrow x = 500.4 = 2000\\\dfrac{y}{3} = 500 \Rightarrow y = 500.3 = 1500\\\dfrac{z}{1} = 500 \Rightarrow z = 500.1 = 500\end{array} \right.\)

Vậy khối lượng rác thải mỗi loại là \(2000g\) rác tái chế, \(1500g\) rác không tái chế và \(500g\) chất thải nguy hại.

Bài 5 (VD):

Phương pháp:

Áp dụng tính chất phép cộng phân số, lũy thừa và giả thiết \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{a}\) để thu gọn biểu thức.

Cách giải:

\(Do\,\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{a}\,\) nên áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{a}\, = \dfrac{{a + b + c}}{{b + c + a}} = 1\) hay \(a = b = c\)

\(M = \dfrac{{{a^{2019}} + {b^{2019}} + {c^{2019}}}}{{{a^{672}}{b^{673}}{c^{674}}}}\)\( = \dfrac{{{a^{2019}} + {a^{2019}} + {a^{2019}}}}{{{a^{672}}{a^{673}}{a^{674}}}} = \dfrac{{3{a^{2019}}}}{{{a^{2019}}}} = 3\)

Bài 6 (VD):

Phương pháp:

- Nhớ lại kiến thức về các trường hợp bằng nhau của tam giác rồi chứng minh.

Chú ý : Hai tam giác bằng nhau có các cặp cạnh và cặp góc tương ứng bằng nhau.

- Tiên đề Ơ-clit : Qua một điểm nằm ngoài đường thẳng a ta chỉ vẽ được một và chỉ một đường thẳng song song với đường thẳng a.

Cách giải:

Cho tam giác \(ABC\) có \(AB = AC\) và \(AB > BC.\) Gọi \(M\) là trung điểm của cạnh \(BC.\)

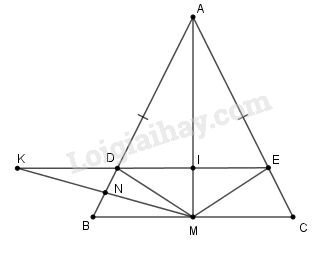
a) Chứng minh \(\Delta ABM = \Delta ACM\) và \(AM \bot BC.\)

 Xét  \(\Delta ABM\) và \(\Delta ACM\) có :

\(AB = AC\left( {gt} \right)\)

\(AM\) là cạnh chung 

\(BM = MC\) (do \(M\) là trung điểm của \(BC\))

Vậy \(\Delta ABM = \Delta ACM\left( {c - c - c} \right)\)

\( \Rightarrow \widehat {AMB} = \widehat {AMC}\) (cặp góc tương ứng)         (1)

Mà \(M \in BC\)nên \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)         (2)

Từ (1), (2) ta có : \(\widehat {AMB} + \widehat {AMC} = 2\widehat {AMB} = 180^\circ \)\( \Rightarrow \widehat {AMB} = \dfrac{{180^\circ }}{2}\)

Hay \(AM \bot BC\).

b) Trên cạnh \(AB\) lấy điểm \(D,\) trên cạnh \(AC\) lấy điểm \(E\) sao cho \(AD = AE.\) Chứng minh \(MD = ME.\)

Xét \(\Delta ADM\) và \(AEM\) có :

\(AD = AE\left( {gt} \right)\)

\(\widehat {DAM} = \widehat {EAM}\) (cặp góc tương ứng của hai tam giác bằng nhau – câu a)

\(AM\) là cạnh chung

\( \Rightarrow \Delta DAM = \Delta EAM\left( {c - g - c} \right)\)

\( \Rightarrow MED = ME\) (cặp cạnh tương ứng)

c) Gọi \(N\) là trung điểm của đoạn thẳng \(BD.\) Trên tia đối của tia \(NM\) lấy điểm \(K\) sao cho \(NK = NM.\) Chứng minh các điểm \(K,D,E\) thẳng hàng.

Gọi \(DE \cap AM = \left\{ I \right\}\)

\(\Delta ADI\) và \(\Delta AEI\) có :

+ Cạnh chung\(AI\)

+ \(AD = AE\left( {gt} \right)\)

+ \(\widehat {DAI} = \widehat {EAI}\) (chứng minh ở câu a)

\( \Rightarrow \Delta ADI = \Delta AEI\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {DIA} = \widehat {EIA}\) (cặp góc tương ứng)

Mà \(\widehat {DIA} + \widehat {EIA} = 180^\circ \) nên \(\widehat {DIA} = \widehat {EIA} = \dfrac{{180^\circ }}{2} = 90^\circ \) hay \(DE \bot AM\)

Mặt khác \(BC \bot AM\)

Suy ra : \(DE//BC\) (3)

Nối \(KD\)

Xét \(\Delta KDN\) và \(\Delta MBN\) có :

+ \(ND = NB\) (\(N\) là trung điểm của \(BD\))

+ \(\widehat {KND} = \widehat {MNB}\) (đối đỉnh)

+ \(NK = NM\) (cách vẽ)

\( \Rightarrow \Delta KDN = \Delta MBN\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {DKN} = \widehat {BMN}\) (cặp góc tương ứng)

Hay \(KD//BM\) (có cặp góc so le trong bằng nhau)

Mà \(M \in BC\) nên \(KD//BC.\)        (4)

Từ (3), (4) suy ra \(K,D,E\) cùng nằm trên một đường thẳng song song với \(BC\) hay \(K,D,E\) thẳng hàng (tiên đề Ơ-clit).

HẾT