Giải đề thi học kì 1 toán lớp 7 năm 2020 - 2021 THCS Quỳnh Phương

Câu 1 (2,0 điểm) Thực hiện phép tính

\(a)\,\,\frac{3}{7} + \frac{{27}}{{25}}\, + \frac{4}{7} - \frac{2}{{25}}\)

\(b)\,{5^3}:{5^2} + {2^2}.4 - {5^2}\)

\(c)\left| {\frac{{ - 3}}{4}} \right|:{( - 3)^2} - \sqrt {\frac{{16}}{9}} \)

Câu 2 (2,0 điểm) Tìm x, biết:

\(a)\,3x + 5 = 8\)

\(b)\,\frac{x}{9} = \frac{4}{x}\)

\(c)\,\,\left| {2x - 1} \right| = 3\)

Câu 3 (2,5 điểm)

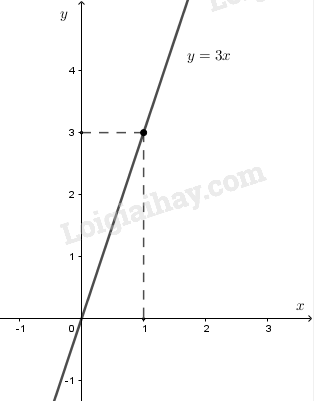
a) Vẽ đồ thị hàm số y = 3x

b) Lớp 7A có 45 học sinh, lớp có tỉ lệ học sinh giỏi, học sinh khá, học sinh trung bình tỉ lệ 2:3:4. Tính số học sinh ứng với từng xếp loại học lực.

Câu 4 (3 điểm)

Cho tam giác ABC vuông tại A. Gọi I là trung điểm của cạnh BC. Trên tia đối của tia IA lấy điểm E sao cho IE = IA. Chứng minh rằng:

a) \(\Delta AIB = \Delta EIC\)

b) EC//AB

c) BC = 2 AI

Câu 5 (0,5 điểm) Tìm giá trị lớn nhất của biểu thức:

\(A = \left| {x - 2021} \right| - \left| {x - 2020} \right|\)

LỜI GIẢI CHI TIẾT

Câu 1:

\(\begin{array}{l}a)\,\,\frac{3}{7} + \frac{{27}}{{25}}\, + \frac{4}{7} - \frac{2}{{25}} = \left( {\,\frac{3}{7} + \frac{4}{7}} \right) + \left( {\frac{{27}}{{25}} - \frac{2}{{25}}} \right)\\ = 1 + 1 = 2\end{array}\)

\(\begin{array}{l}b)\,{5^3}:{5^2} + {2^2}.4 - {5^2} = 5 + 4.4 - 25\\ = 5 + 16 - 25 = 21 - 25 =  - 4\end{array}\)

\(\begin{array}{l}c)\left| {\frac{{ - 3}}{4}} \right|:{( - 3)^2} - \sqrt {\frac{{16}}{9}}  = \frac{3}{4}:9 - \frac{4}{3}\\ = \frac{3}{4}.\frac{1}{9} - \frac{4}{3} = \frac{1}{{12}} - \frac{{16}}{{12}} =  - \frac{{15}}{{12}}\end{array}\)

Câu 2:

\(\begin{array}{l}a)\,3x + 5 = 8\\\,\,\,\,\,3x = 8 - 5\\\,\,\,\,3x = 3\\\,\,\,\,\,\,x = 1\end{array}\)

Vậy x = 1

\(\begin{array}{l}b)\,\frac{x}{9} = \frac{4}{x} \Leftrightarrow x.x = 4.9\\ \Leftrightarrow {x^2} = 36 \Leftrightarrow x =  \pm 6\end{array}\)

Vậy \(x =  \pm 6\)

\(\begin{array}{l}c)\,\,\left| {2x - 1} \right| = 3 \Rightarrow \left[ {\begin{array}{*{20}{c}}{2x - 1 = 3}\\{2x - 1 =  - 3}\end{array}} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{2x = 4}\\{2x =  - 2}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 2}\\{x =  - 1}\end{array}} \right.\end{array}\)

Vậy \(x \in \left\{ { - 1;2} \right\}\)

Câu 3:

a) Đồ thị hàm số y=2x+3 đi qua điểm (0;0) và (1;3)

b) Gọi số học sinh giỏi, khá và trung bình lần lượt là x; y; z ( \(x,y,z \in {\mathbb{N}^*}\))

Do lớp có tỉ lệ học sinh giỏi, học sinh khá, học sinh trung bình tỉ lệ 2:3:4 nên ta có:

\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4}\)

Do lớp 7A có 45 học sinh nên: \(x + y + z = 45\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{2} = \frac{y}{3} = \frac{z}{4} = \frac{{x + y + z}}{{2 + 3 + 4}} = \frac{{45}}{9} = 5\)

+) \(\frac{x}{2} = 5 \Rightarrow x = 10\)

+) \(\frac{y}{3} = 5 \Rightarrow y = 15\)

+) \(\frac{z}{4} = 5 \Rightarrow z = 20\)

Vậy số học sinh giỏi, khá và trung bình lần lượt là 10; 15; 20

Câu 4:

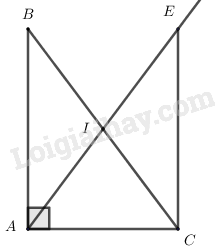
a) Xét \(\Delta AIB\) và \(\Delta EIC\) có:

IE = IA (gt)

\(\widehat {BIA} = \widehat {EIC}\) (đối đỉnh)

IB = IC (I là trung điểm của BC)

=> \(\Delta AIB\) = \(\Delta EIC\) (c.g.c)

b) Do \(\Delta AIB\) = \(\Delta EIC\) nên \(\widehat {ABI} = \widehat {BCE}\) (2 góc tương ứng)

Mà hai góc này ở vị trí so le trong nên EC//AB (đpcm)

c) Do EC//AB mà \(AB \bot AC\)

=> \(AC \bot EC\)

Xét \(\Delta ABC\) và \(\Delta CEA\) có:

AB = EC ( do \(\Delta AIB\) = \(\Delta EIC\))

\(\widehat {BAC} = \widehat {ECA} = {90^0}\)

AC chung

=> \(\Delta ABC\)=\(\Delta CEA\) (c.g.c)

=> AE = BC

Mà \(AE = 2AI(gt)\) suy ra \(BC = 2AI\).

Câu 5:

Ta có: \(\left| {a - b} \right| \ge \left| a \right| - \left| b \right|\)

Nên: \(A = \left| {x - 2021} \right| - \left| {x - 2020} \right| \le \left| {x - 2021 - \left( {x - 2020} \right)} \right| = 1\)

Vậy GTLN của A bằng 1 khi x = 2020.