Giải câu hỏi trắc nghiệm trang 160 sách bài tập toán 11 - Chân trời sáng tạo tập 1
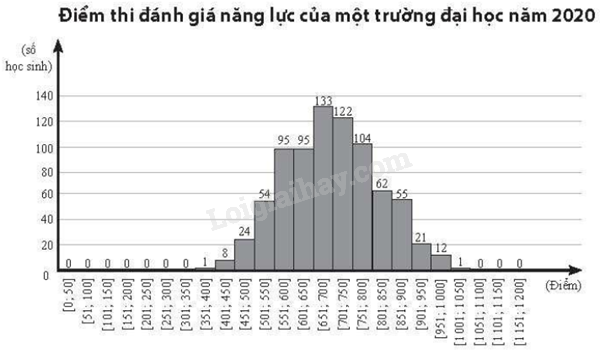
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây. Tổng số học sinh tham gia kì thi đánh giá năng lực trên là A. 780. B. 787. C. 696. D. 697.
Câu 1
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
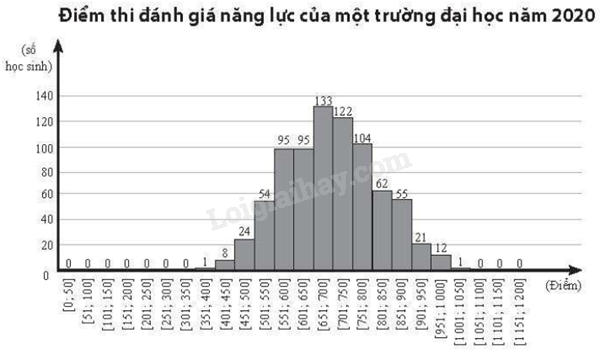
Tổng số học sinh tham gia kì thi đánh giá năng lực trên là
A. 780.
B. 787.
C. 696.
D. 697.
Phương pháp giải:
Để tính tổng số học sinh tham gia kì thi, đếm xem mỗi khoảng điểm có bao nhiêu học sinh tham gia, rồi cộng tổng lại.
Lời giải chi tiết:
Tổng số học sinh tham gia kì thi đánh giá năng lực là:
\(1 + 8 + 24 + 54 + 95 + 95 + 133 + 122 + 104 + 62 + 55 + 21 + 12 + 1 = 787\) (học sinh)
Chọn B
Câu 2
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
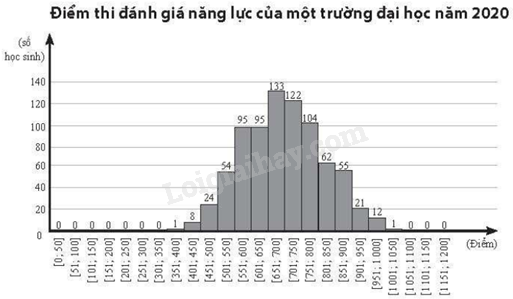
Giá trị đại diện cho nhóm chứa mốt của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Sử dụng kiến thức về nhóm chứa một của mẫu số liệu để tính: Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Lời giải chi tiết:
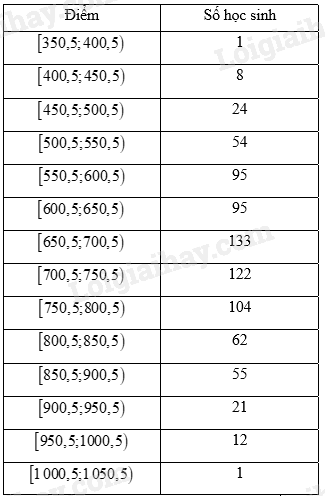
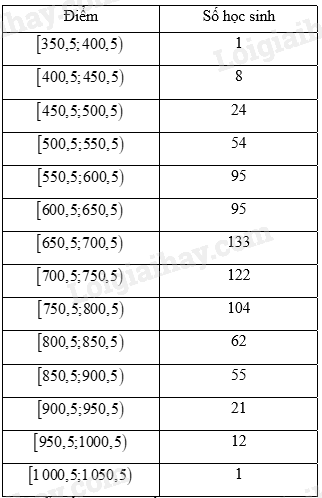
Bảng số liệu ghép nhóm hiệu chỉnh:
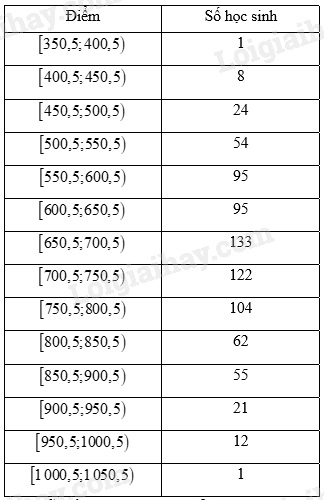
Nhóm chứa mốt của mẫu số liệu ghép nhóm là \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B.
Câu 3
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
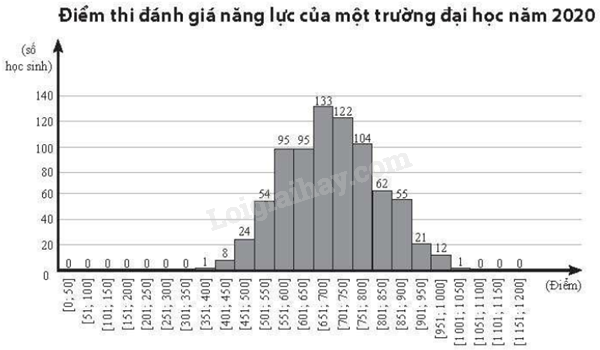
Giá trị đại diện cho nhóm chứa trung vị của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa trung vị, ta đi tìm trung vị của mẫu số liệu rồi xét xem trung vị đó thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:
Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Vì \(n = 787\) nên trung vị của mẫu số liệu là \({x_{394}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B
Câu 4
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
Giá trị đại diện cho nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ nhất, ta đi tìm tứ phân vị thứ nhất rồi xét xem t tứ phân vị thứ nhất thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:
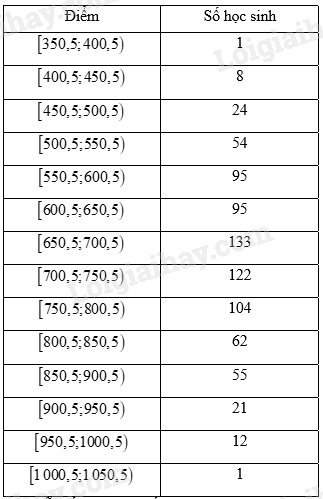
Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là \({x_{197}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {600,5;650,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {600,5;650,5} \right)\) là: \(\frac{1}{2}\left( {600,5 + 650,5} \right) = 625,5\)
Chọn A
Câu 5
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
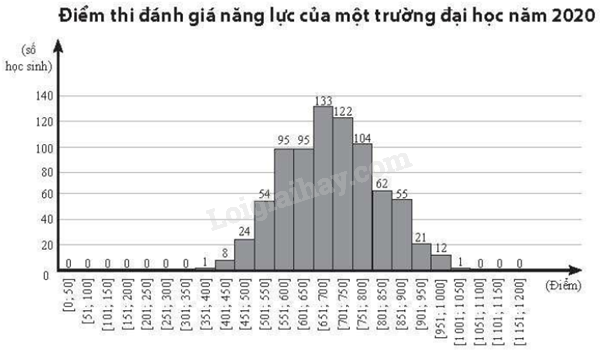
Giá trị đại diện cho nhóm chứa tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ ba, ta đi tìm tứ phân vị thứ ba rồi xét xem tứ phân vị thứ ba thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:
Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ ba của mẫu số liệu là \({x_{591}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {750,5;800,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {750,5;800,5} \right)\) là: \(\frac{1}{2}\left( {750,5 + 800,5} \right) = 775,5\)
Chọn D
Câu 6
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

160,5 là giá trị đại diện cho nhóm
A. 2.
B. 3.
C. 4.
D. 5.
Phương pháp giải:
Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
Lời giải chi tiết:
Giá trị đại diện của nhóm \(\left[ {159;162} \right)\) là: \(\frac{1}{2}\left( {159 + 162} \right) = 160,5\)
Vậy 160,5 là giá trị đại diện cho nhóm 4.
Chọn C
Câu 7
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 157,76.
B. 158,25.
C. 157,5.
D. 160,28.
Phương pháp giải:
Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải chi tiết:
Nhóm chứa mốt của mẫu số liệu là nhóm \(\left[ {156;159} \right)\).
Do đó, \({u_m} = 156,{n_{m - 1}} = 13,{n_m} = 40,{n_{m + 1}} = 21,{u_{m + 1}} = 159\)
Mốt của mẫu số liệu trên là:
\({M_O} = 156 + \frac{{40 - 13}}{{\left( {40 - 13} \right) + \left( {40 - 21} \right)}}.\left( {159 - 156} \right) \approx 157,76\)
Chọn A
Câu 8
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Trung vị của mẫu số liệu ghép nhóm trên là
A. 157,76.
B. 157,25.
C. 158,25.
D. 160,45.
Phương pháp giải:
Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên trung vị của mẫu số liệu là \(\frac{{{x_{50}} + {x_{51}}}}{2}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e} = 156 + \frac{{\frac{{100}}{2} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 158,25\)
Chọn C
Câu 9
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 156,25.
B. 157,5.
C. 156,38.
D. 157,54.
Phương pháp giải:
Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{{{x_{25}} + {x_{26}}}}{2}\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 156 + \frac{{\frac{{100}}{4} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 156,375 \approx 156,38\)
Chọn C
Câu 10
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 160,52.
B. 161,52.
C. 161,14.
D. 162,25.
Phương pháp giải:
Sử dụng kiến thức về tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{{{x_{75}} + {x_{76}}}}{2}\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {159;162} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 159 + \frac{{\frac{{3.100}}{4} - \left( {7 + 13 + 40} \right)}}{{21}}.\left( {162 - 159} \right) \approx 161,14\)
Chọn C
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải câu hỏi trắc nghiệm trang 160 sách bài tập toán 11 - Chân trời sáng tạo tập 1 timdapan.com"







