Bài 9.3 phần bài tập bổ sung trang 95 SBT toán 8 tập 1
Giải bài 9.3 phần bài tập bổ sung trang 95 sách bài tập toán 8. Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.
Đề bài
Cho hình thang cân \(ABCD,\) đường cao \(AH.\) Gọi \(E,\, F\) theo thứ tự là trung điểm của các cạnh bên \(AD,\, BC.\) Chứng minh rằng \(EFCH\) là hình bình hành.
Phương pháp giải - Xem chi tiết
Tính chất đường trung bình của hình thang
Tính chất tam giác vuông (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Lời giải chi tiết
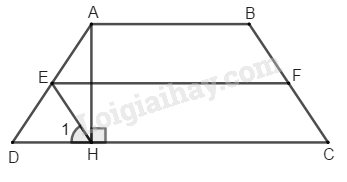
Ta có: \(E\) là trung điểm của \(AD\) (gt)
\(F\) là trung điểm của \(BC\) (gt)
Nên \(EF\) là đường trung bình của hình thang \(ABCD\)
\(⇒ EF // CD\) hay \(EF // CH\) (*)
\(∆ AHD\) vuông tại \(H\) có \(HE\) là đường trung tuyến ứng với cạnh huyền \(AD.\)
Ta có: \(HE = ED = \dfrac{1}{2}AD\) (tính chất tam giác vuông)
\(⇒ ∆ EDH\) cân tại \(E\)
\( \Rightarrow \widehat D = {\widehat H_1}\) (tính chất tam giác cân)
\(\widehat D = \widehat C\) (vì ABCD là hình thang cân)
Suy ra: \({\widehat H_1} = \widehat C\)
\(⇒ EH // CF\) (**) (vì có cặp góc đồng vị bằng nhau)
Từ (*) và (**) suy ra tứ giác \(EFCH\) là hình bình hành (1 cặp cạnh song song và bằng nhau).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9.3 phần bài tập bổ sung trang 95 SBT toán 8 tập 1 timdapan.com"







