Bài 108 trang 93 SBT toán 8 tập 1
Giải bài 108 trang 93 sách bài tập toán 8. Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm (làm tròn kết quả đến chữ số thập phân thứ nhất)
Đề bài
Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng \(5\,cm\) và \(10\,cm\) (làm tròn kết quả đến chữ số thập phân thứ nhất)
Phương pháp giải - Xem chi tiết
Áp dụng định lí Py - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
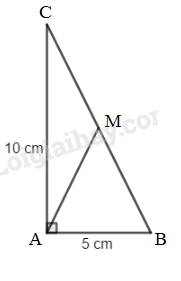
Giả sử \(∆ ABC\) có \(\widehat A = {90^0}\) , \(M\) là trung điểm của \(BC;\) \(AB = 5cm;\, AC = 10cm.\) Theo định lý Py-ta-go trong tam giác ABC vuông tại A, ta có:
\(\eqalign{ & B{C^2} = A{B^2} + A{C^2} }\)
\(\Rightarrow BC = \sqrt {{5^2} + {{10}^2}} = \sqrt {125}\) \(\approx 11,2(cm) \)
Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên \(AM =\eqalign {1 \over 2} BC\) (tính chất tam giác vuông)
\(⇒ AM \approx \eqalign{1 \over 2}.11,2 = 5,6\) \((cm)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 108 trang 93 SBT toán 8 tập 1 timdapan.com"