Bài 119 trang 94 SBT toán 8 tập 1
Giải bài 119 trang 94 sách bài tập toán 8. Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.
Đề bài
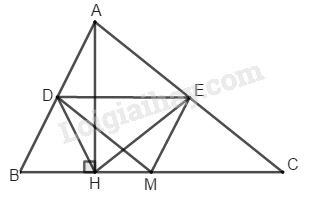
Cho tam giác \(ABC,\) đường cao \(AH.\) Gọi \(D,\, E,\, M\) theo thứ tự là trung điểm của \(AB,\, AC,\, BC.\) Chứng minh rằng tứ giác \(DEMH\) là hình thang cân.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
+ Vì \(D\) là trung điểm của \(AB\) (gt)
\(E\) là trung điểm của \(AC\) (gt)
nên \(DE\) là đường trung bình của tam giác \(ABC\)
\(⇒ DE // BC\) hay \(DE // HM\)
Suy ra: Tứ giác \(DEMH\) là hình thang
+ Vì \(D\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(BC\) (gt)
nên \(DM\) là đường trung bình của \(∆ BAC\)
\(⇒ DM = \dfrac{1}{2}AC\) (tính chất đường trung bình của tam giác) (1)
Trong tam giác vuông \(AHC\) có \(\widehat {AHC} = {90^0}\).
\(HE\) là đường trung tuyến ứng với cạnh huyền \(AC.\)
\(⇒ HE = \dfrac{1}{2}AC\) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(DM = HE\)
Vậy hình thang \(DEMH\) là hình thang cân (vì có hai đường chéo bằng nhau \(DM=EH)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 119 trang 94 SBT toán 8 tập 1 timdapan.com"







