Bài 121 trang 95 SBT toán 8 tập 1
Giải bài 121 trang 95 sách bài tập toán 8. Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DH
Đề bài
Cho tam giác nhọn \(ABC,\) các đường cao \(BD, CE.\) Gọi \(H,\, K\) theo thứ tự là chân các đường vuông góc kẻ từ \(B,\, C\) đến đường thẳng \(DE.\) Chứng minh rằng \(EH = DK\)
HD: Vẽ điểm \(I\) là trung điểm của \(DE,\) điểm \(M\) là trung điểm của \(BC.\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất đường trung bình của tam giác
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông: Trong tam giác vuông đường trung tuyến tuyến ứng với cạnh huyền bằng nửa cạnh ấy
Lời giải chi tiết
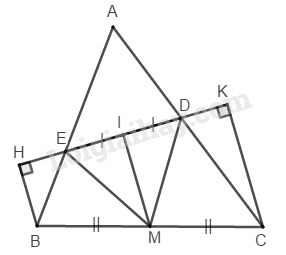
Ta có: \(BH ⊥ DE\) (gt)
\(CK ⊥ DE\) (gt)
Suy ra \(BH // CK\) nên tứ giác \(BHKC\) là hình thang
Ta có: Gọi \(M\) là trung điểm của \(BC,\) \(I\) là trung điểm của \(DE\)
Trong tam giác \(BDC\) vuông tại \(D\) có \(DM\) là trung tuyến ứng với cạnh huyền \(BC.\)
\(⇒ DM = \dfrac{1}{2} BC\) (tính chất tam giác vuông)
Trong tam giác \(BEC\) vuông tại \(E\) có \(EM\) là đường trung tuyến ứng với cạnh huyền \(BC.\)
\(⇒ DM = \dfrac{1}{2} BC\) (tính chất tam giác vuông)
Suy ra: \(DM = EM\) nên \(∆ MDE\) cân tại \(M\)
\(∆ MDE\) cân tại \(M\) có \(MI\) là đường trung tuyến nên \(MI\) là đường cao \(⇒ MI ⊥ DE\)
Suy ra: \(MI // BH // CK\) (cùng vuông góc với DE)
Xét hình thang \(BHKC\) có \(MI // BH // CK\) và \(BM = MC\)
Suy ra: \(HI = IK\) (tính chất đường trung bình hình thang)
\(⇒ HE + EI = ID + DK\)
mà \(EI = ID\) ( theo cách vẽ)
\(⇒ HE = DK\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 121 trang 95 SBT toán 8 tập 1 timdapan.com"







