Bài 117 trang 94 SBT toán 8 tập 1
Giải bài 117 trang 94 sách bài tập toán 8. Chứng minh rằng ba điểm C, B, D trên hình 18 thẳng hàng.
Đề bài
Chứng minh rằng ba điểm \(C,\, B,\, D\) trên hình 18 thẳng hàng.
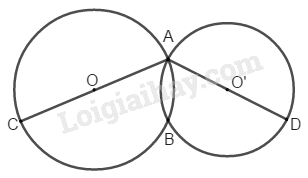
Phương pháp giải - Xem chi tiết
Sử dụng:
Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.
Lời giải chi tiết
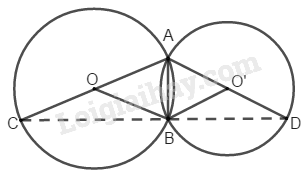
Nối \(AB,\, BO,\, BC,\, BO’,\, BD.\)
Trong \(∆ ABC\) ta có:
\(OA = OC = R\) (bán kính đường tròn \((O)\))
Nên \(BO\) là đường trung tuyến của \(∆ ABC\)
Mà \(BO = R\) (bán kính \((O)\))
\(⇒ BO = OA = OC = \dfrac{1}{2}AC\)
Nên tam giác \(ABC\) vuông tại \(B\) \( \Rightarrow \widehat {ABC} = {90^0}\)
Trong \(∆ ABD\) ta có: \(AO’ = O’D = R’\) (bán kính \((O’)\))
Nên \(BO’\) là đường trung tuyến của \(∆ ABD\)
Mà \(BO’ = R’\) (bán kính \((O’)\)) \(⇒ BO’ = AO’ = O’D = \dfrac{1}{2}AD\)
Nên tam giác \(ABD\) vuông tại \(B\) \( \Rightarrow \widehat {ABD} = {90^0}\)
\(\widehat {ABC} + \widehat {ABD} = \widehat {CBD}\)
\( \Rightarrow \widehat {CBD} = {90^0} + {90^0} = {180^0}\)
Vậy \(C,\, B,\, D\) thẳng hàng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 117 trang 94 SBT toán 8 tập 1 timdapan.com"







