Giải bài 8 trang 31 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{\sin i}}{{\sin r}}\), với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường.
Đề bài
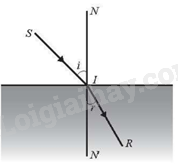
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{\sin i}}{{\sin r}}\), với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là \({45^o}\) thì góc khúc xạ bằng \({30^o}\). Khi góc tới là \({60^o}\) thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phương trình lượng giác cơ bản để giải: Phương trình \(\sin x = m\) có nghiệm khi \(\left| m \right| \le 1\). Khi đó, nghiệm của phương trình là \(x = \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\); \(x = \pi - \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\) với \(\alpha \) là góc thuộc \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\).
Lời giải chi tiết
Theo đầu bài ta có: \(\frac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \frac{{\sin {{60}^0}}}{{\sin r}} \) \( \Leftrightarrow \sin r = \frac{{\sin {{60}^0}.\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{{\sqrt 6 }}{4}\)
Suy ra: \(r \approx 37,{76^0}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 31 sách bài tập toán 11 - Chân trời sáng tạo tập 1 timdapan.com"







