Giải bài 8 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Một chất điểm dao động điều hòa theo phương trình \(s = 3\sin \left( {\frac{\pi }{2}t} \right)\) với s tính bằng cm và t tính bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì \(s \le - \frac{3}{2}\).
Đề bài
Một chất điểm dao động điều hòa theo phương trình \(s = 3\sin \left( {\frac{\pi }{2}t} \right)\) với s tính bằng cm và t tính bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì \(s \le - \frac{3}{2}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số \(y = \sin u\left( x \right)\) để giải.
Lời giải chi tiết
Trong 4 giây đầu, ta có \(0 \le t \le 4\), suy ra: \(0 \le \frac{\pi }{2}t \le 2\pi \).
Đặt \(x = \frac{\pi }{2}t\), khi đó \(x \in \left[ {0;2\pi } \right]\). Đồ thị của hàm số \(y = \sin x\) trên đoạn \(\left[ {0;2\pi } \right]\) là:
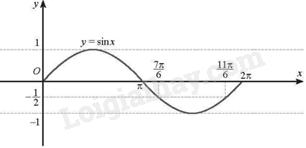
Dựa vào đồ thị trên đoạn \(\left[ {0;2\pi } \right]\), ta có:
\(s \le \frac{{ - 3}}{2}\) khi \(3\sin x \le \frac{{ - 1}}{2}\), suy ra \(\frac{{7\pi }}{6} \le x \le \frac{{11\pi }}{6}\). Do đó, \(\frac{7}{3} \le t \le \frac{{11}}{3}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 27 sách bài tập toán 11 - Chân trời sáng tạo tập 1 timdapan.com"