Giải bài 7 trang 119 SGK Toán 7 tập 2 - Cánh diều
Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.
Đề bài
Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.
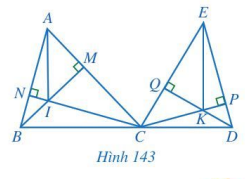
Phương pháp giải - Xem chi tiết
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải chi tiết
Ta có:
I là giao điểm của hai đường cao BM, CN trong tam giác ABC. Suy ra I là trực tâm của tam giác ABC. Vậy \(AI \bot BC\). (1)
K là giao điểm của hai đường cao DQ, CP trong tam giác CED. Suy ra K là trực tâm của tam giác CED.
Vậy \(EK \bot CD\). (2)
Mà ba điểm B, C, D thẳng hàng. (3)
Từ (1), (2) và (3) suy ra: AI // EK.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 7 trang 119 SGK Toán 7 tập 2 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 7 trang 119 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







