Giải bài 5 trang 119 SGK Toán 7 tập 2 - Cánh diều
Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh: a) Nếu OM = ON thì AM // BN; b) Nếu AM // BN thì OM = ON.
Đề bài
Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh:
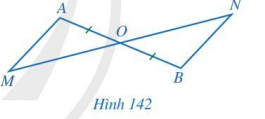
a) Nếu OM = ON thì AM // BN;
b) Nếu AM // BN thì OM = ON.
Phương pháp giải - Xem chi tiết
Chứng minh dựa vào chứng minh hai tam giác AOM và BON bằng nhau.
Lời giải chi tiết
a) Xét tam giác AOM và tam giác BON có:
OA = OB;
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
OM = ON.
Vậy \(\Delta AOM = \Delta BON\)(c.g.c).
Suy ra: \(\widehat {AMO} = \widehat {BNO}\) (2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên AM // BN.
b) Ta có: AM // BN nên \(\widehat {MAO} = \widehat {NBO}\)(hai góc so le trong).
Xét tam giác AOM và tam giác BON có:
\(\widehat {MAO} = \widehat {NBO}\)
OA = OB;
\(\widehat {AOM} = \widehat {BON}\)(đối đỉnh);
Vậy \(\Delta AOM = \Delta BON\)(g.c.g). Suy ra: OM = ON ( 2 cạnh tương ứng).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 trang 119 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







