Giải bài 14 trang 120 SGK Toán 7 tập 2 - Cánh diều
Cho tam giác nhọn ABC có AB < AC. Hai đường cao AD và CE cắt nhau tại H. Khi đó
Đề bài
Cho tam giác nhọn ABC có AB < AC. Hai đường cao AD và CE cắt nhau tại H. Khi đó
A.\(\widehat {HAB} = \widehat {HAC}\). B.\(\widehat {HAB} > \widehat {HAC}\). C.\(\widehat {HAB} = \widehat {HCB}\). D.\(\widehat {HAC} = \widehat {BAC}\).
Phương pháp giải - Xem chi tiết
Trpng một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
Lời giải chi tiết
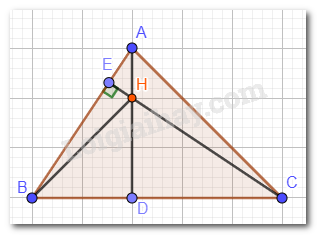
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC đều vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\)hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: loại đáp án A, B, D.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 14 trang 120 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







