Bài 6.53 trang 192 SBT đại số 10
Giải bài 6.53 trang 192 sách bài tập đại số 10. Chứng minh các đẳng thức...
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
LG a
a) A = 2(sin6α + cos6α) - 3(sin4α + cos4α)
Lời giải chi tiết:
A = 2(sin2α + cos2α)(sin4α + cos4α - sin2αcos2α) - 3(sin4α + cos4α)
= -sin4α - cos4α - 2sin2αcos2α
= -(sin2α + cos2α)2 = -1
Cách khác:
A = 2(sin6α + cos6α) - 3(sin4α + cos4α)
=2[ (sin2α + cos2α)3-3 sin2α.cos2α(sin2α + cos2α)] -3[(sin2α + cos2α)2-2sin2α.cos2α]
=2[1-3 sin2α.cos2α]-3[1-2sin2α.cos2α]
=2-6 sin2α.cos2α-3+6 sin2α.cos2α
=-1
LG b
b) B = 4(sin4α + sin4α) - cos4α
Lời giải chi tiết:
b) A = 4[(sin2α + cos2α)2 - 2sin2αcos2α] - cos4α
=4[1-2sin2αcos2α] - cos4α
=4-8 sin2αcos2α- cos4α
=4-2.(2sinα.cosα)2 – (1 - 2sin22α)
=4 – 2 sin22α - 1 + 2sin22α = 3
LG c
c) C = 8(cos8α - sin8α) - cos6α - 7cos2α
Lời giải chi tiết:
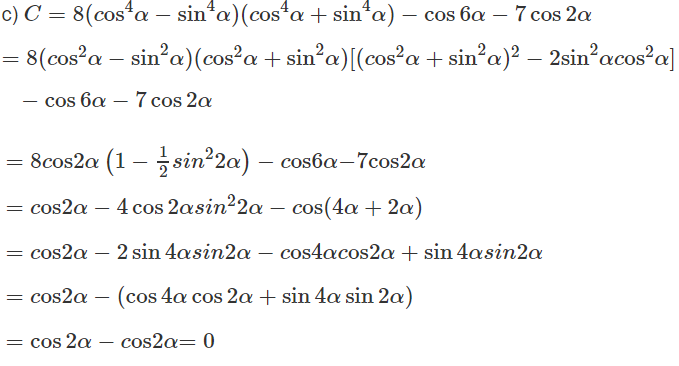
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6.53 trang 192 SBT đại số 10 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 6.53 trang 192 SBT đại số 10 timdapan.com"







