Bài 61 trang 101 Vở bài tập toán 7 tập 2

Đề bài

Cho tam giác \(ABC\) với \(AC < AB.\) Trên tia đối của tia \(BC\) lấy điểm \(D\) sao cho \(BD = AB.\) Trên tia đối của tia \(CB\) lấy điểm \(E\) sao cho \(CE = AC.\) Vẽ các đoạn thẳng \(AD, AE.\)

a) Hãy so sánh góc \(ADC\) và góc \(AEB.\)

b) Hãy so sánh các đoạn thẳng \(AD\) và \(AE.\)

Lời giải chi tiết

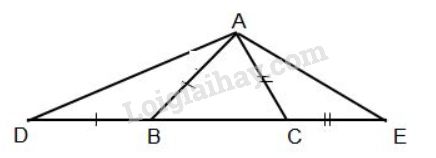
a) Tam giác \(ABC\) có \(AC < AB\) (theo giả thiết) nên \(\widehat {ACB} > \widehat {ABC}\) (1) (quan hệ giữa cạnh và góc đối diện trong tam giác).

\(BD = BA\) (theo giả thiết) nên tam giác \(ABD\) cân tại \(B\), do đó \(\widehat {ADB} = \widehat {DAB}\).

Góc \(ABC\) là góc ngoài ở đỉnh \(B\) của tam giác \(ABD\) nên

\(\widehat {ABC}  =  \widehat {ADB} +  \widehat {DAB}\) hay \(\widehat B  = 2 \widehat D\)  (2)

\(CE=CA\) (theo giả thiết) nên tam giác \(ACE\) cân ở đỉnh, do đó \(\widehat {CAE} = \widehat {CEA}\).

Góc \(ACB\) là góc ngoài ở đỉnh \(C\) của tam giác \(ACE\) hay \(\widehat C = 2\widehat E \)  (3)

Từ (1), (2), (3) suy ra \(\widehat {ADC} < \widehat {AEB}\) 

b) Trong tam giác \(AED\), ta có  \(\widehat {ADE} < \widehat {AED}\) (theo câu a)

Suy ra \( AD > AE\) (quan hệ giữa góc - cạnh đối diện trong một tam giác).