Bài 6 trang 116 Vở bài tập toán 7 tập 2

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\); đường phân giác \(BE\). Kẻ \(EH\) vuông góc với \(BC\) (\(H \in BC)\). Gọi \(K\) là giao điểm của \(AB\) và \(HE.\) Chứng minh rằng:

a) \(∆ABE= ∆HBE.\)

b) \(BE\) là đường trung trực của đoạn thẳng \(AH.\)

c) \(EK = EC.\)

d) \(AE < EC.\)

Lời giải chi tiết

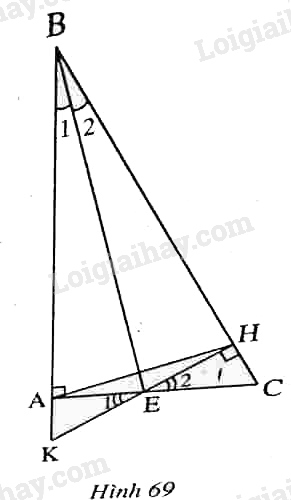
 a) Hai tam giác vuông \(ABE\) và \(HBE\) có \(BE \) là cạnh huyền chung, \(\widehat {{B_1}} = \widehat {{B_2}}\) (\(BE\) là tia phân giác của góc \(B\)), do đó \(∆ABE = ∆HBE\)  (cạnh huyền-góc nhọn)

b) Từ \(∆ABE = ∆HBE\) suy ra \(BA = BH,\)\( EA = EH\), theo tính chất đường trung trực của đoạn thẳng ta có \(BE\) là đường trung trực của đoạn thẳng \(AH.\)

c) Do \(EA = EH\), \(\widehat {{E_1}} = \widehat {{E_2}}\), \(\widehat {A} = \widehat {H} = {90^{\circ}}\) nên \(∆AEK = ∆HEC \) (g.c.g), suy ra \(EK = EC\).

d) Trong tam giác vuông \(AEK\), \(EK\) là cạnh huyền nên \(AE < EK\) mà \(EK= EC\) (câu c) nên \(AE < EC\).