Giải bài 5 trang 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Đề bài

Cho hình chóp S. ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, \(AC = 2a,BD = 2b\); tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho \(AI = x\left( {0 < x < a} \right)\) , (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD).

a) Xác định giao tuyến của mặt phẳng (P) với các mặt của hình chóp S. ABCD.

b) Tính diện tích hình tạo bởi các đoạn giao tuyến ở câu a theo a, b và x.

Lời giải chi tiết

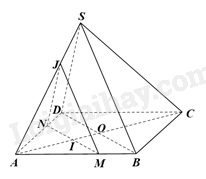
a) Trong mặt phẳng (ABCD), qua I kẻ đường thẳng song song với BD cắt AB tại M, cắt AD tại N.

Trong mặt phẳng (SAD), kẻ NJ//SD (J thuộc SA)

Vì MN//BD, \(BD \subset \left( {SBD} \right)\), MN không nằm trong mặt phẳng (SBD) nên MN//(SBD).

Vì JN//SD, \(SD \subset \left( {SBD} \right)\), JN không nằm trong mặt phẳng (SBD) nên JN//(SBD).

Mà JN và MN cắt nhau tại N và nằm trong mặt phẳng (MNJ) nên (SBD)//(MNJ).

Do đó, mặt phẳng (P) là mặt phẳng (MNJ).

Khi đó, \(\left( P \right) \cap \left( {SAB} \right) = JM,\left( P \right) \cap \left( {SAD} \right) = JN,\left( P \right) \cap \left( {ABCD} \right) = NM\)

b) Các giao tuyến của mặt phẳng (P) với các mặt của hình chóp tạo thành tam giác MNJ.

Vì tam giác JMN đồng dạng với tam giác SBD nên tam giác JMN là tam giác đều.

Ta có: MN//BD nên \(\frac{{MN}}{{BD}} = \frac{{AI}}{{AO}} = \frac{x}{a} \Rightarrow MN = \frac{{2bx}}{a}\)

Do đó, diện tích tam giác MNJ là:

\(S = \frac{1}{2}MN.MJ.\sin \widehat {NMJ} = \frac{1}{2}M{N^2}.\sin {60^0} = \frac{1}{2}.{\left( {\frac{{2bx}}{a}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{{b^2}{x^2}\sqrt 3 }}{{{a^2}}}\)