Giải bài 1 trang 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho hình bình hành ABCD. Từ các đỉnh A, B, C và D lần lượt kẻ các tia Ax, By, Cz, Dt song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt).
Đề bài
Cho hình bình hành ABCD. Từ các đỉnh A, B, C và D lần lượt kẻ các tia Ax, By, Cz, Dt song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh mặt phẳng (Ax, By) song song với mặt phẳng (Cz, Dt).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết
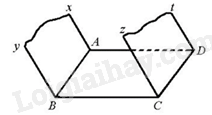
Vì Cz//By, \(By \subset \left( {Ax,By} \right)\), Cz không nằm trong mặt phẳng (Ax, By) nên Cz// (Ax, By).
Vì tứ giác ABCD là hình bình hành nên AB//CD. Mà \(AB \subset \left( {Ax,By} \right)\), CD không nằm trong mặt phẳng (Ax, By) nên CD// (Ax, By).
Vì Cz// (Ax, By), CD// (Ax, By), Cz và CD cắt nhau tại C và nằm trong mặt phẳng (Cz, Dt) nên (Cz, Dt) // (Ax, By).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 1 trang 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1 timdapan.com"







