Giải bài 4 trang 73 SGK Toán 7 tập 2 - Cánh diều
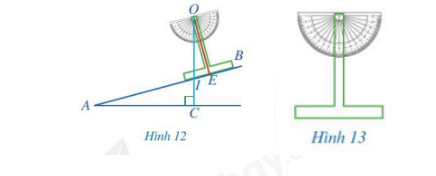
Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bới đường thẳng AB và phương nằm ngang AC, người ta làm như sau: - Làm một thước chữ T như Hình 13; - Đặt thước chữ T dọc theo cạnh AB như Hình 12, \(OE \bot AB\); - Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi); - Tính góc BAC, biết rằng dây dọi OI tạo
Đề bài
Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bới đường thẳng AB và phương nằm ngang AC, người ta làm như sau:
- Làm một thước chữ T như Hình 13;
- Đặt thước chữ T dọc theo cạnh AB như Hình 12, \(OE \bot AB\);
- Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);
- Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.
Phương pháp giải - Xem chi tiết
Muốn tính góc BAC, ta xét tam giác IAC:
- Tổng số đo ba góc trong tam giác này bằng 180°. → Tính số đo góc AIC.
- Góc AIC bằng góc OIE (hai góc này đối đỉnh).
- Muốn tính số đo góc OIE ta xét tam giác OIE, tổng 3 góc trong tam giác này bằng 180°.
Lời giải chi tiết
Ta có, trong tam giác OIE: \(\widehat I + 15^\circ + 90^\circ = 180^\circ \).
Suy ra: \(\widehat {OIE} = \widehat {AIC} = 180^\circ - 90^\circ - 15^\circ = 75^\circ \).
Vậy góc BAC bằng: \(90^\circ - 75^\circ = 15^\circ \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 73 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







