Bài 37 trang 71 SBT toán 9 tập 1

LG a

Cho các điểm \(M(-1 ; -2)\), \(N(-2; -4)\), \(P(2; -3)\), \(Q(3; -4,5)\). Tìm tọa độ của các điểm \(M’, N’, P’, Q’\) lần lượt đồi xứng với các điểm \(M, N, P, Q\) qua trục \(Ox.\)

Phương pháp giải:

* Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

* Để vẽ đồ thị \(y = \left| {f(x)} \right|\)

Ta có: 

\(y = \left| f(x) \right| = \left\{ \matrix{
f(x)\,\,\,\,\,\,\,\,nếu\,\,\,f(x) \ge 0 \hfill \cr 
- f(x)\,\,\,\,\,\,\,nếu\,\,\,f(x) \le 0 \hfill \cr} \right.\)

Vẽ đồ thị \( y= f(x)\) với \(f(x) \ge 0\) (1)

Vẽ đồ thị \( y= - f(x)\) với \(f(x)<0\) (2)

Đồ thị \(y = \left| {f(x)} \right|\) là hợp của hai đồ thị (1) và (2).

Lời giải chi tiết:

Hình a

 

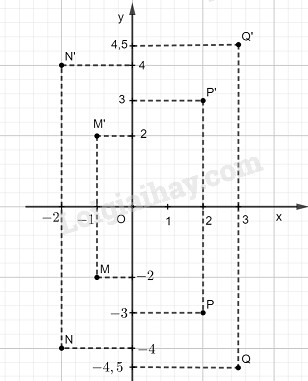
Tọa độ các điểm \(M’, N’, P’ , Q’\)   lần lượt đối xứng với các điểm \(M , N, P, Q\) qua trục \(Ox\):

\(M'\left( {1 - ;2} \right),N'\left( { - 2;4} \right),\)\(P'\left( {2;3} \right),Q'\left( {3;4,5} \right)\)

---

LG b

Vẽ đồ thị của các hàm số sau trên cùng hệ trục tọa độ: 

\(\eqalign{
& y = \left| x \right| \cr 
& y = \left| {x + 1} \right| \cr} \) .

Phương pháp giải:

* Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

* Để vẽ đồ thị \(y = \left| {f(x)} \right|\)

Ta có: 

\(y = \left| f(x) \right| = \left\{ \matrix{
f(x)\,\,\,\,\,\,\,\,nếu\,\,\,f(x) \ge 0 \hfill \cr 
- f(x)\,\,\,\,\,\,\,nếu\,\,\,f(x) \le 0 \hfill \cr} \right.\)

Vẽ đồ thị \( y= f(x)\) với \(f(x) \ge 0\) (1)

Vẽ đồ thị \( y= - f(x)\) với \(f(x)<0\) (2)

Đồ thị \(y = \left| {f(x)} \right|\) là hợp của hai đồ thị (1) và (2).

Lời giải chi tiết:

Hình b

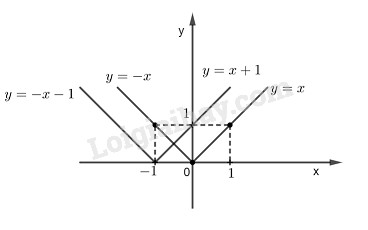
*Ta có:

\(y = \left| x \right| = \left\{ \matrix{
x\,\,\,\,\,\,\,\,nếu\,\,\,x \ge 0 \hfill \cr 
- x\,\,\,\,\,\,\,nếu\,\,\,x \le 0 \hfill \cr} \right.\)

Đồ thị hàm số \(y = x\) đi qua gốc tọa độ O và điểm \((1;1)\)

Đồ thị hàm số \(y = -x\) đi qua gốc tọa độ O và điểm \((-1;1)\)

* Ta có :

\(y = \left| {x + 1} \right| \)\(= \left\{ \matrix{
x + 1\,\,\,\,\,\,nếu\,\,\,x \ge - 1 \hfill \cr 
- \left( {x + 1} \right)\,nếu\,\,\,x \le - 1 \hfill \cr} \right.\)

- Vẽ đồ thị hàm số \(y = x + 1\)

Cho \(x = 0\) thì \(y = 1.\) Ta có: \((0;1)\)

Cho \(y = 0\) thì \(x = -1.\) Ta có: \((-1;0)\)

Đồ thị hàm số \(y = x + 1\) đi qua hai điểm \((0;1)\) và \((-1;0)\)

- Vẽ đồ thị hàm số \(y = - (x + 1)\)

Cho \(x = 0\) thì \(y = -1.\) Ta có : \((0;-1)\)

Cho \(y = 0\) thì \(x = -1.\) Ta có : \((-1;0)\)

Đồ thị hàm số \(y = - (x + 1)\) đi qua hai điểm \((0;-1)\) và \((-1;0)\)

---

LG c

Tìm tọa độ giao điểm của đồ thị của các hàm số \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\).

Từ đó , suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất.

Phương pháp giải:

* Để biểu diễn điểm \(M({x_0};{y_0})\) trên mặt phẳng tọa độ ta làm như sau:

- Vẽ đường thẳng song song với trục Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M({x_0};{y_0})\).

* Để vẽ đồ thị \(y = \left| {f(x)} \right|\)

Ta có: 

\(y = \left| f(x) \right| = \left\{ \matrix{
f(x)\,\,\,\,\,\,\,\,nếu\,\,\,f(x) \ge 0 \hfill \cr 
- f(x)\,\,\,\,\,\,\,nếu\,\,\,f(x) \le 0 \hfill \cr} \right.\)

Vẽ đồ thị \( y= f(x)\) với \(f(x) \ge 0\) (1)

Vẽ đồ thị \( y= - f(x)\) với \(f(x)<0\) (2)

Đồ thị \(y = \left| {f(x)} \right|\) là hợp của hai đồ thị (1) và (2).

Lời giải chi tiết:

Ta có : \(y = x\) và \(y = x + 1\) song song với nhau

             \(y = -x\) và \(y = -(x + 1)\) song song với nhau

Suy ra chỉ có đồ thị hàm số \(y = -x\) và \(y = x + 1\) cắt nhau

Phương trình hoành độ giao điểm: 

\( - x = x + 1 \Leftrightarrow 2x =  - 1 \Leftrightarrow x =  - \dfrac{1}{2}\)

Suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất.

Tung độ giao điểm: \(y =  - x \Rightarrow y = \dfrac{1}{2}\)

Vậy tọa độ giao điểm của đường thẳng \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\) là : \(I\left( { - \dfrac{1}{2};\dfrac{1 }{2}} \right)\)