Bài 3 trang 5 SBT toán 8 tập 2
Giải bài 3 trang 5 sách bài tập toán 8. Cho ba biểu thức 5x – 3 ; x^2 – 3x + 12 và (x + 1)(x – 3). Lập ba phương trình, mỗi phương trình có hai vế là hai trong ba biểu thức đã cho ...
Đề bài
Cho ba biểu thức \(5x - 3\), \({x^2} - 3x + 12\) và \(\left( {x + 1} \right)\left( {x - 3} \right)\)
a) Lập ba phương trình, mỗi phương trình có hai vế là hai trong ba biểu thức đã cho.
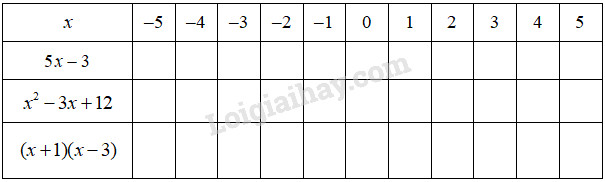
b) Hãy tính giá trị của các biểu thức đã cho khi \(x\) nhận tất cả các giá trị thuộc tập hợp \(M = \{x ∈ ℤ | - 5 ≤ x ≤ 5 \}\), điền vào bảng sau rồi cho biết mỗi phương trình ở câu a) có những nghiệm nào trong tập hợp M :
Phương pháp giải - Xem chi tiết
a) Sử dụng: Một phương trình với ẩn \(x\) có dạng \(A(x) = B(x)\), trong đó vế trái \(A(x)\) và vế phải \(B(x)\) là hai biểu thức của cùng một biến \(x.\)
b) Từ \(M=\{x ∈ ℤ | - 5 ≤ x ≤ 5\}\) suy ra: \(x \in \left\{ { - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5} \right\}\)
Thay các giá trị của \(x\) vào các biểu thức đã cho, từ bảng giá trị của các biểu thức ta tìm được nghiệm của các phương trình.
Lời giải chi tiết
a) Ba phương trình lập được là:
(1): \(5x - 3 = {x^2} - 3x + 12\)
(2): \({x^2} - 3x + 12 = \left( {x + 1} \right)\left( {x -3} \right)\)
(3): \(5x - 3 = \left( {x + 1} \right)\left( {x - 3} \right)\)
b) Từ \(M=\{x ∈ ℤ | - 5 ≤ x ≤ 5\}\) suy ra: \(x \in \left\{ { - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5} \right\}\)
Ta có bảng sau :
Phương trình (1) có nghiệm là \(x = 3\) và \(x = 5\).
Phương trình (2) không có nghiệm.
Phương trình (3) có nghiệm là \(x = 0\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 5 SBT toán 8 tập 2 timdapan.com"