Giải bài 27 trang 90 sách bài tập toán 9 - Cánh diều tập 1
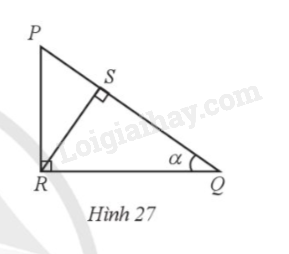
Cho tam giác PQR vuông tại R có đường cao RS và \(\widehat Q = \alpha \) (Hình 27). Ti số lượng giác \(\sin \alpha \) bằng:
Đề bài
Cho tam giác PQR vuông tại R có đường cao RS và \(\widehat Q = \alpha \) (Hình 27). Ti số lượng giác \(\sin \alpha \) bằng:
A. \(\frac{{PR}}{{RS}}\)
B. \(\frac{{PR}}{{QR}}\)
C. \(\frac{{PS}}{{RS}}\)
D. \(\frac{{RS}}{{QR}}\)
Phương pháp giải - Xem chi tiết
Dựa vào tỉ số lượng giác: \(\sin \alpha \) = cạnh đối / cạnh huyền.
Lời giải chi tiết
Do RS là đường cao của tam giác PRQ nên \(\widehat {RSQ} = 90^\circ \).
Xét tam giác RSQ vuông tại S, ta có: \(\sin Q = \sin \alpha = \frac{{RS}}{{RQ}}\).
Đáp án D.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 27 trang 90 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 27 trang 90 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"