Bài 1.10 trang 8 SBT giải tích 12

Đề bài

Hàm số \(y = \sqrt {25 - {x^2}} \) nghịch biến trên khoảng:

A. \(\left( { - \infty ;0} \right)\)

B. \(\left( { - 5;0} \right)\)

C. \(\left( {0;5} \right)\)

D. \(\left( {5; + \infty } \right)\)

Lời giải chi tiết

TXĐ: \(D = \left[ { - 5;5} \right]\).

Ta có: \(y' = \dfrac{{ - x}}{{\sqrt {25 - {x^2}} }} = 0 \Leftrightarrow x = 0\).

Bảng biến thiên:

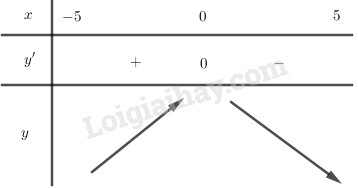
Hàm số đã cho nghịch biến trên \(\left( {0;5} \right)\).

Chọn C.