Bài 110 trang 153 SBT toán 7 tập 1

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có \(\displaystyle {{AB} \over {AC}} = {3 \over 4}\) và \(BC=15cm.\) Tính các độ dài \(AB, AC.\)

Lời giải chi tiết

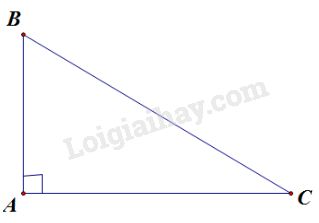
Theo đề bài, ta có:

\(\displaystyle {{AB} \over {AC}} = {3 \over 4} \)

\(\displaystyle \Rightarrow {{AB} \over 3} = {{AC} \over 4}\)

\(\displaystyle \Rightarrow {{A{B^2}} \over 9} = {{A{C^2}} \over {16}}\)

Áp dụng định lí Pytago vào tam giác vuông \(ABC\), ta có:

\(B{C^2} = A{B^2} + A{C^2}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\displaystyle {{A{B^2}} \over 9} = {{A{C^2}} \over {16}} = {{A{B^2} + A{C^2}} \over {9 + 16}}\)\(\,=\dfrac{{B{C^2}}}{{25}} = \dfrac{{{{15}^2}}}{{25}} = \dfrac{{225}}{{25}} = 9\)

\( \Rightarrow A{B^2} = 9.9 = 81 \Rightarrow AB = 9\left( {cm} \right)\) (vì \(AB > 0\))

\( \Rightarrow A{C^2} = 16.9 = 144\)\(\,\Rightarrow AC = 12\left( {cm} \right)\) (vì \(AC > 0\)).