Bài 109 trang 153 SBT toán 7 tập 1

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), kẻ \(BH \bot \,AC\). Gọi \(D\) là một điểm thuộc cạnh đáy \(BC.\) Kẻ \({\rm{D}}E \bot\, AC,DF \bot\, AB\). Chứng minh rằng \(DE + DF = BH.\)

Lời giải chi tiết

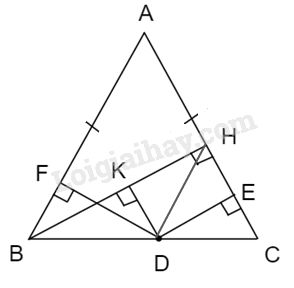
Kẻ \({\rm{DK}} \bot {\rm{BH}}\)

\(BH \bot AC\;\left( {gt} \right)\)

\( \Rightarrow DK // AC\) (vì cùng vuông góc với \(BH\))

\( \Rightarrow \widehat {K{\rm{D}}B} = \widehat C\) (hai góc đồng vị)

Vì \(∆ABC\) cân tại \(A\) nên \(\widehat B = \widehat C\) (tính chất tam giác cân)

\( \Rightarrow \widehat {K{\rm{D}}B} = \widehat B\)

Xét hai tam giác vuông \(BFD\) và \(DKB\) có:

\(\widehat {BF{\rm{D}}} = \widehat {DKB} = 90^\circ \)

\(BD\) cạnh chung

\(\widehat {FB{\rm{D}}} = \widehat {K{\rm{D}}B}\) (chứng minh trên)  

\( \Rightarrow  ∆BFD = ∆DKB\) (cạnh huyền - góc nhọn)

\( \Rightarrow  DF = BK \) (hai cạnh tương ứng)            (1)

Nối \(DH.\)

Vì \(DK//AC\) nên \(\widehat {EH{\rm{D}}} = \widehat {K{\rm{D}}H}\) (hai góc so le trong)

Xét \(∆DEH\) và \(∆HKD\) có:

\(\widehat {DEH} = \widehat {HKD} = 90^\circ \)

\(DH\) cạnh chung

\(\widehat {EH{\rm{D}}} = \widehat {K{\rm{D}}H}\) (chứng minh trên)

\( \Rightarrow ∆DEH = ∆HKD\) (cạnh huyền - góc nhọn)

\( \Rightarrow DE = HK\) (hai cạnh tương ứng)              (2)

Mặt khác:   \(BH = BK + HK\)                                       (3)

Từ (1), (2) và (3) suy ra \( DF + DE = BH\).