Giải bài 10 trang 53 sách bài tập toán 9 - Cánh diều tập 1
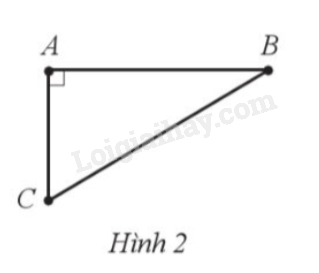
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí A đến trường. Trường của anh An ở vị trí B và trường của em Bình ở vị trí C theo hai hướng vuông góc với nhau (Hình 2). Anh An đi với tốc độ 4 km/h và đến trưởng sau 15 phút. Em Bình đi với tốc độ 3 km/h và đến trường sau 12 phút. Tính khoảng cách BC giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
Đề bài
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí A đến trường. Trường của anh An ở vị trí B và trường của em Bình ở vị trí C theo hai hướng vuông góc với nhau (Hình 2). Anh An đi với tốc độ 4 km/h và đến trưởng sau 15 phút. Em Bình đi với tốc độ 3 km/h và đến trường sau 12 phút. Tính khoảng cách BC giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng công thức \(s = v.t\) để tính quãng đường AB,AC.
Bước 2: Áp dụng định lý Pythagore trong tam giác vuông ABC để tính BC.
Lời giải chi tiết
Đổi 15 phút = 0,25 giờ; 12 phút = 0,2 giờ.
Quãng đường AB là \(4.0,25 = 1\left( {km} \right).\)
Quãng đường AC là \(3.0,2 = 0,6\left( {km} \right).\)
Áp dụng định lý Pythagore trong tam giác vuông ABC ta có:
\(C{B^2} = A{B^2} + A{C^2} = {1^2} + 0,{6^2} = 1,36\), do đó \(CB = \sqrt {1,36} \) hay \(CB \approx 1,17\)km.
Vậy khoảng cách BC giữa hai trường khoảng 1,17km.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 10 trang 53 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"