Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 3 - Hình học 9

Đề bài

Cho hình vuông ABCD. Trên các cạnh BC, CD lần lượt lấy các điểm E và F sao cho \(\widehat {EAF} = 45^\circ \). Gọi P và Q theo thứ tự là giao điểm  của các đoạn thẳng AE, AF với đường chéo BD. Chứng minh rằng ∆AQE vuông cân.

Lời giải chi tiết

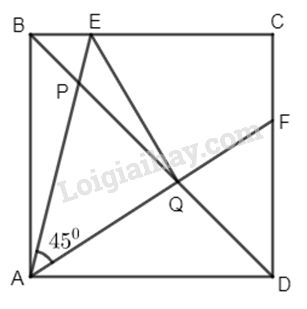
Ta có \(\widehat {EBQ} = \widehat {EAQ} = 45^\circ \) nên A, B cùng nằm trên cung chứa góc 45º vẽ trên đoạn EQ hay bốn điểm A, B, E, Q cùng nằm trên một đường tròn.

Lại có \(\widehat {ABE} = 90^\circ  \Rightarrow \widehat {AQE} = 90^\circ \) hay \(∆AQE\) vuông tại Q có \(\widehat {EAQ} = 45^\circ \).

Vậy \(∆AQE\) vuông cân.