Bài 51 trang 87 SGK Toán 9 tập 2

Đề bài

Cho \(I, \, O\) lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác \(ABC\) với \(\widehat{A} = 60^0.\) Gọi \(H\) là giao điểm của các đường cao \(BB'\) và \(CC'.\)

Chứng minh các điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn.

Lời giải chi tiết

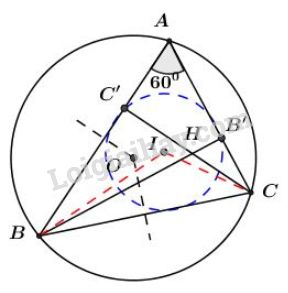
+) Ta có: \(\widehat{BOC} = 2\widehat{BAC} =  2.60^0= 120^0\)  (góc nội tiếp và góc ở tâm cùng chắn một cung \(BC\)).                (1)

+) Lại có  \(\widehat{BHC} = \widehat{B'HC'}\) (hai góc đối đỉnh) 

Mà \(\widehat{B'HC'} = 360^\circ  - \widehat {HC'A} - \widehat {HB'A} - \widehat A\) \( = 360^\circ  - 90^\circ  - 90^\circ  - 60^\circ  = 120^\circ\)

\(\Rightarrow \widehat{BHC} = 120^0.\)           (2)  

+) Vì I là tâm đường tròn nội tiếp tam giác ABC nên BI; CI lần lượt là tia phân giác góc B, góc C.

Xét tam giác \(ABC\) có \(\widehat B + \widehat C + \widehat A = 180^\circ  \Leftrightarrow \widehat B + \widehat C = 180^\circ  - 60^\circ  = 120^\circ \)

Xét tam giác BIC theo định lý về tổng 3 góc trong một tam giác ta có

\(\begin{array}{l}\widehat {BIC} = 180^\circ  - \widehat {IBC} - \widehat {ICB} = 180^\circ  - \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}\\ = 180^\circ  - \dfrac{{\widehat B + \widehat C}}{2} = 180^\circ  - 60^\circ  = 120^\circ \end{array}\)

Do đó \(\widehat{BIC} = 120^0.\)  (3)

Từ (1), (2), (3) ta thấy các điểm \(O, \, H, \, I\) cùng nằm trên các cung chứa góc \(120^0\) dựng trên đoạn thẳng \(BC.\) Nói cách khác, năm điểm \(B,\, C,\, O,\, H,\, I\) cùng thuộc một đường tròn.