Bài 64 trang 15 SBT Hình học 11 Nâng cao
Giải bài 64 trang 15 sách bài tập Hình học 11 Nâng cao. Cho hai điểm A và A’ đối xứng với nhau qua điểm I, F là phép dời hình biến I thành I, biến A thành A’. Chứng minh rằng F là phép đối xứng tâm hoặc đối xứng trục.
Đề bài
Cho hai điểm A và A’ đối xứng với nhau qua điểm I, F là phép dời hình biến I thành I, biến A thành A’. Chứng minh rằng F là phép đối xứng tâm hoặc đối xứng trục.
Lời giải chi tiết
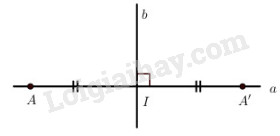
Gọi a là đường thẳng đi qua A và A’, b là đường thẳng đi qua I và vuông góc với a.
Theo giả thiết F biến a thành chính nó, do đó F cũng biến b thành chính. Có thể xảy ra hai trương hợp:
- Mỗi điểm của b biến thành chính nó. Khi đó rõ ràng F là phép đối xứng qua đường thẳng b.
- Mỗi điểm của b biến thành điểm đối xứng qua I. Khi đó tương tự như bài tập 14, ta có thể chứng minh rằng F là phép đối xứng qua tâm I.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 64 trang 15 SBT Hình học 11 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 64 trang 15 SBT Hình học 11 Nâng cao timdapan.com"







