Bài tập 24 trang 136 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho hình 68. Chứng minh rằng tứ giác EFGH là hình thoi.

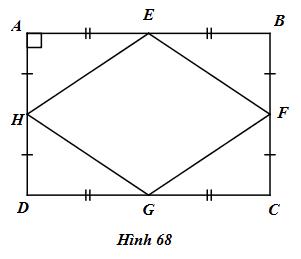
Lời giải chi tiết

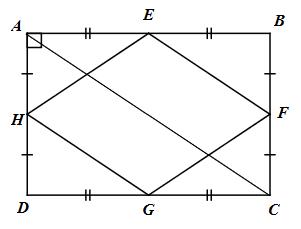
E, F lần lượt là trung điểm của AB và BC

\( \Rightarrow EF\) là đường trung bình của tam giác ABC

\( \Rightarrow EF//AC\) và \(EF = {1 \over 2}AC\,\,\,\left( 1 \right)\)

H, G lần lượt là trung điểm của AD và DC

\( \Rightarrow HG\) là đường trung bình của tam giác ACD

\( \Rightarrow HG//AC\) và \(HG = {1 \over 2}AC\) (2)

Từ (1) và (2) \( \Rightarrow EF//HG\) và \(EF = HG\).

Vậy tứ giác EFGH là hình bình hành.

Tứ giác ABCD có \(AB = CD\) và \(AD = BC \Rightarrow \) Tứ giác ABCD là hình bình hành.

Mà \(\widehat {BAD} = {90^0} \Rightarrow ABCD\) là hình chữ nhật.

Xét \(\Delta EBF\) và \(\Delta CGF\) có :

\(\eqalign{  & EB = EC\,\,\left( {gt} \right)  \cr  & BF = FC\,\,\left( {gt} \right)  \cr  & \widehat {EBF} = \widehat {GCF}\,\,\left( { = {{90}^0}} \right)  \cr  &  \Rightarrow \Delta EBF = \Delta GCF\,\,\left( {c.g.c} \right) \Rightarrow EF = GF \cr} \)

Chứng minh tương tự ta có \(GF = GH,\,\,GH = EF \Rightarrow EF = GF = GH = EH\)

Do đó tứ giác EFGH là hình thoi.