Bài tập 21 trang 136 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho góc nhọn xOy. Trên tia Õ lần lượt lấy các điểm A, B, C, D sao cho OA = AB = BC = CD. Từ A, B, C, D lần lượt kẻ các đường thẳng vuông góc với Oy, chúng lần lượt cắt Oy tại M, N, E, F.

a) Chứng minh rằng  \(OM = {1 \over 4}OF\)

b) Biết AM = 3 cm. Tính DF.

Lời giải chi tiết

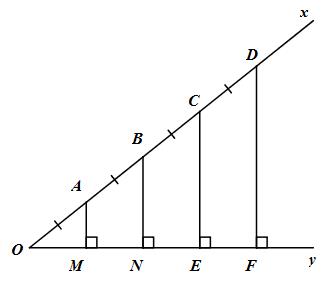
a) Ta có: AM // BN // CE // DF (cùng vuông góc với Oy)

Và \(OA = AB = BC = CD\,\,\left( {gt} \right)\)

Do đó AM, BN, CE, DF là các đường thẳng song song cách đều.

\( \Rightarrow OM = MN = NE = EF\)

Mà \(OM + MN + NE + EF = OF \Rightarrow OM = MN = NE = EF = {1 \over 4}OF\)

b) \(\Delta ODF\) có:

B là trung điểm của OD \(\left( {OB = BD} \right)\)

N là trung điểm của OF \(\left( {ON = NF} \right)\)

\( \Rightarrow BN\) là đường trung bình của tam giác ODF \( \Rightarrow BN = {1 \over 2}DF\)

\(\Delta OBN\) có:

A là trung điểm của OB \(\left( {OA = AB} \right)\)

M là trung điểm của ON \(\left( {OM = MN} \right)\)

\( \Rightarrow AM\) là đường trung bình của tam giác OBN \( \Rightarrow AM = {1 \over 2}BN\)

Mà \(BN = {1 \over 2}DF \Rightarrow AM = {1 \over 2}.{1 \over 2}DF = {1 \over 4}DF\)

\( \Rightarrow DF = 4AM \Rightarrow DF = 4.3 = 12\,\,\left( {cm} \right)\)